Понятие многогранника
Многогранником называется геометрическое тело в пространстве, которое ограниченно несколькими многоугольниками.
Примеры многогранников Вы можете видеть на рисунке 1.
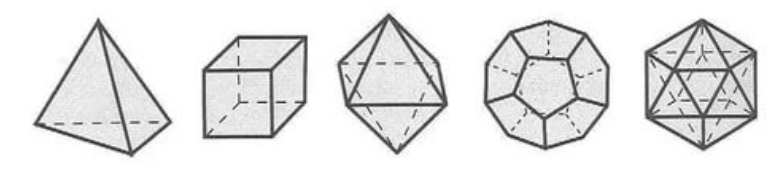
Рисунок 1. Примеры многогранников
При этом многоугольники, из которых состоят многогранники, называют гранями многогранника, стороны многоугольников -- сторонами многогранника, а вершины многоугольников -- вершинами многогранника.
Если многогранник всегда будет лежать по одну сторону от любой плоскости его граней, то многогранник называется выпуклым (рис. 2).
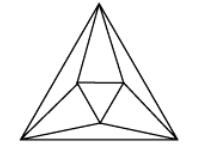
Рисунок 2. Выпуклый многогранник
Рассмотрим далее детально, как пример выпуклого многогранника, призму.
Призма
Геометрическая фигура, образованная двумя равными $n-$угольниками, лежащими в параллельных плоскостях, вершины которых соединены между собой так, что соответствующая вершина первого $n-$угольника соединена с соответствующей вершиной второго $n-$уголника, называется призмой (рис. 3).
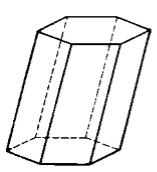
Рисунок 3. Призма
Параллельные $n-$уголники называются основаниями призмы, параллелограммы их соединяющие -- боковыми гранями, стороны параллелограммов -- сторонами призмы, а вершины $n-$угольников -- вершинами призмы.
В зависимости от количества углов в основании призмы ее можно назвать треугольной, четырехугольной и так далее (рис. 4).
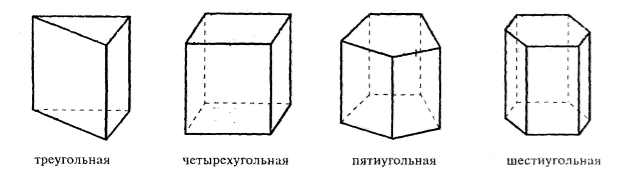
Рисунок 4.
Отметим, что параллелепипед является частным случаем четырехугольной призмы.
Призма, у которой все двугранные углы равны ${90}^0$ называется прямой (рис. 5). В противном же случае она является наклонной.
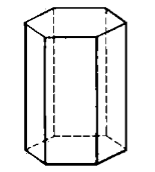
Рисунок 5. Прямая призма
Прямая призма, в основании которой лежат правильные $n-$уголники называется правильной (рис. 6).
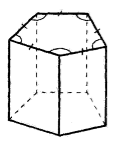
Рисунок 6.
Площадь призмы
Полная площадь призмы определяется следующим образом
где $S_{бок}$ - сумма площадей всех ее боковых граней, а $S_{осн}$ - площадь основания данной призмы.
Рассмотрим и докажем следующую теорему.
Площадь боковой поверхности прямой призмы определяется как произведение периметра основания данной призмы на ее высоту.
Доказательство.
Рассмотрим прямую $n-$угнольную призму, длины оснований которой равны $a_1,\ a_2,\dots ,a_n$ соответственно. Как мы знаем, высота прямой призмы равняется боковой стороне данной призмы. Обозначим её через $h$. Тогда, так как боковые грани являются прямоугольниками, площади боковых граней равняются, соответственно
\[S_1=a_1h,\ {S_2=a}_2h,\dots ,{S_n=a}_nh\]Так как площадь боковой поверхности -- сумма площадей всех боковых граней, то
\[S_{бок}=S_1+S_2+\dots +S_n=a_1h+a_2h+\dots +a_nh=h\left(a_1+a_2+\dots +a_n\right)=P_{осн}h\]Теорема доказана.
Объем призмы
Объем призмы определяется как произведение площади основания этой призмы на высоту.
Доказательство.
Рассмотрим произвольную призму, проведем в ней высоту и построим ось $Ox$ через эту высоту, считая началом координат точку $O$ основания высоты (рис. 7).
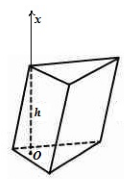
Рисунок 7.
Проводя сечения, перпендикулярно $Ox$ будем получать многоугольники с $S\left(x\right)=S_{осн}$. Используя формулу для вычисления объема тел, получим
\[V=\int\limits^h_0{S_{осн}dx}=S_{осн}{\left.x\right|}^h_0=S_{осн}h-S_{осн}\cdot 0=S_{осн}h\]ч. т. д.
Пример задачи
Найти полную площадь и объем прямой призмы с равнобедренным треугольником при основании и высотой $h=5$, если боковая сторона треугольника равна $2$, а угол между ними равен ${30}^0$.
Решение.
Так как боковая сторона основания равна $2$, а угол между ними равен ${30}^0$. То
\[S_{осн}=\frac{1}{2}\cdot 2\cdot 2\cdot sin{30}^0=2\cdot \frac{1}{2}=1\]По теореме косинуса, третья сторона треугольника равна
\[a=\sqrt{2^2+2^2-2\cdot 2\cdot 2cos{30}^0}=\sqrt{4+4-4\sqrt{3}}=2\sqrt{2-\sqrt{3}}\]По теореме 1
\[S_{бок}=\left(2+2+2\sqrt{2-\sqrt{3}}\right)\cdot 5=10\left(2+\sqrt{2-\sqrt{3}}\right)\]По теореме 2, получим
\[V=1\cdot 5=5\]Ответ: $5$.












