Понятие «объём тела»
Представьте себе ведро с водой. Объём воды в ведре говорит нам, сколько воды на самом деле в нём, а ёмкость ведра говорит, сколько воды оно может в себя вмещать.
Объёмом называется количество пространства, занимаемого телом или веществом.
Для обозначения объёма в формулах используется заглавная латинская буква $V.$
Единицы измерения объёма
Единицей измерения объёма в СИ является кубический метр. Также часто объём измеряется таких производных величинах как литр (кубический дециметр), кубический сантиметр и др. В Великобритании и США используются также внесистемные величины -- галлон, баррель, пинта.
Принцип Кавальери
Строгое обоснование вывода формул для вычисления объёмов тел в стереометрии весьма сложно. Однако этот вопрос может быть решён, если принять без доказательства принцип Кавальери: «Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются равновеликие между собой фигуры, то объёмы этих тел равны».
Мы будем выводить формулу объёмов тел, основываясь на ещё более сильном (и интуитивно понятном) утверждении: «Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как $M:n$, то объёмы данных тел относятся как m:n».
Объём параллелепипеда. Определение параллелепипеда
Параллелепипедом называется призма, в основании которой лежит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них -- параллелограмм.
Отметим, что параллелепипед обладает следующим свойством: «Любая плоскость, проходящая через середину диагонали параллелепипеда, делит этот параллелепипед на два равновеликих многогранника».
Типы параллелепипедов
Существует несколько типов параллелепипедов:
-
Прямой -- параллелепипед, у которого все грани -- прямоугольники;
-
Наклонный -- параллелепипед, у которого боковые грани не перпендикулярны основаниям.
Прямоугольным параллелепипедом называется параллелепипед, у которого все грани - прямоугольники.
Куб -- частный случай параллелепипеда.
Объём параллелепипеда
Объём параллелепипеда можно находить тремя способами, принимая за основание этого параллелепипеда любую его грань, а за его высоту -- расстояние между этой гранью и гранью, ей параллельной. На рисунке 1 изображено все $3$ способа нахождения объёма одного и того же параллелепипеда. На первом за основание берётся стороны $a$ и $b$, за высоту $c$. На втором за основание берётся стороны $c$ и $b$, за высоту $a$. На третьем за основание берётся стороны $a$ и $c$, за высоту $b$.
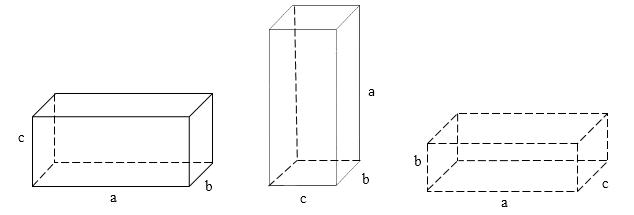
Рисунок 1. Прямоугольный параллелепипед
Сначала мы находим объём прямоугольного параллелепипеда со сторонами основания и высотой равными 1 единицы (рисунок 2а). Объём данного параллелепипеда будет равен 1 кубической единице.
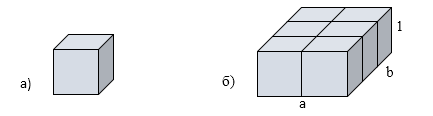
Рисунок 2. Объем каждого твердого тела равен числу единичных кубиков
Теперь возьмём прямоугольный параллелепипед со сторонами основания $a$, $b$ и высотой $1$ (рисунок 2б), расположив данный параллелепипед и единичный куб так, чтобы их основания находились в одной плоскости, а сами многогранники были расположены по одну сторону от этой плоскости.
Тогда площади сечений, образованных при пересечении обоих многогранников любой плоскостью, параллельной плоскости основания этих многогранников, относятся как $(a\cdot b):1$. Это означает, что их объёмы также относятся как $(a\cdot b):1$, т.е.
откуда объём $V_{пар.}$ Прямоугольного параллелепипеда с измерениями $a$, $b$, $1$ равен $a\cdot b\cdot 1$, т.е.
Затем находим объём прямоугольного параллелепипеда с измерениями $a$, $b$, $c$, для чего прямоугольный параллелепипед с измерениями $a$, $b$, $c$ расположим так, чтобы грань со сторонами $1$ и $a$ первого параллелепипеда лежали в одной плоскости, и оба параллелепипеда находились по одну сторону от этой плоскости. Тогда площади сечений, образованных при пересечении обоих многогранников любой плоскостью, параллельной плоскости оснований этих многогранников, относятся как
Это означает, что их объёмы также относятся как $1:c$. А так как объёмы параллелепипеда с измерениями $1$, $a$, $b$ равен $ab$, то для объёма $VF$ прямоугольного параллелепипеда с измерениями $a$, $b$, $c$ выполняется соотношение
Откуда
Объём наклонного параллелепипеда
Проведём через ребро $BC$ плоскость $\alpha $, перпендикулярную основанию $ABCD$ параллелепипеда $ABCD$, и построим треугольную призму (рисунок 3).
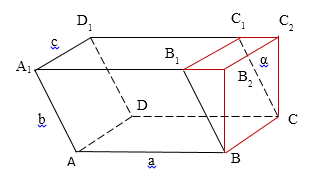
Рисунок 3. Параллелепипед и призма
Теперь через ребро $AD$ проведём плоскость $\beta $, параллельную плоскости $\alpha $ (рисунок 4).
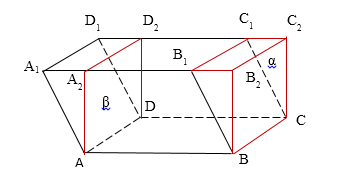
Рисунок 4. Параллелепипед и призма
Этот параллелепипед имеет объём, равный объёму исходного.
Если применить такое преобразования к наклонным граням ещё раз, то получится параллелепипед, у которого все боковые грани перпендикулярны основанию. Снова получился прямоугольный параллелепипед.
Если его подвергнуть подобному преобразованию (сначала дополнить первой призмой, затем отсечь вторую призму), то достроенная и отсекаемая призмы совмещаются параллельным переносом на отрезок AB. Из этого следует, что фигуры имеют одинаковый объём.
Резюмируя проведённые преобразования:
-
сохраняется площадь основания и высота параллелепипеда;
-
плоскости двух боковых граней сохраняются, а две другие становятся перпендикулярными основанию.
Следовательно, объём построенного прямоугольного параллелепипеда равен объёму исходного наклонного.
Объём наклонного параллелепипеда равен произведению площади основания на высоту:

















