Определение длины дуги кривой
Рассмотрим в пространстве дугу $\cup AB$ некоторой кривой. Точками $M_{0} $, $M_{1} $, $M_{2} $, .... , $M_{n-1} $, $M_{n} $ разобьем её на $n$ произвольных последовательных участков. Соединим соседние точки отрезками прямых и получим вписанную в дугу $\cup AB$ ломаную, в которой $M_{0} $ совпадает с точкой $A$, а $M_{n} $ совпадает с точкой $B$. Эта ломаная состоит из звеньев $M_{0} M_{1} $, $M_{1} M_{2} $, .... , $M_{i-1} M_{i} $, .... , $M_{n-1} M_{n} $.
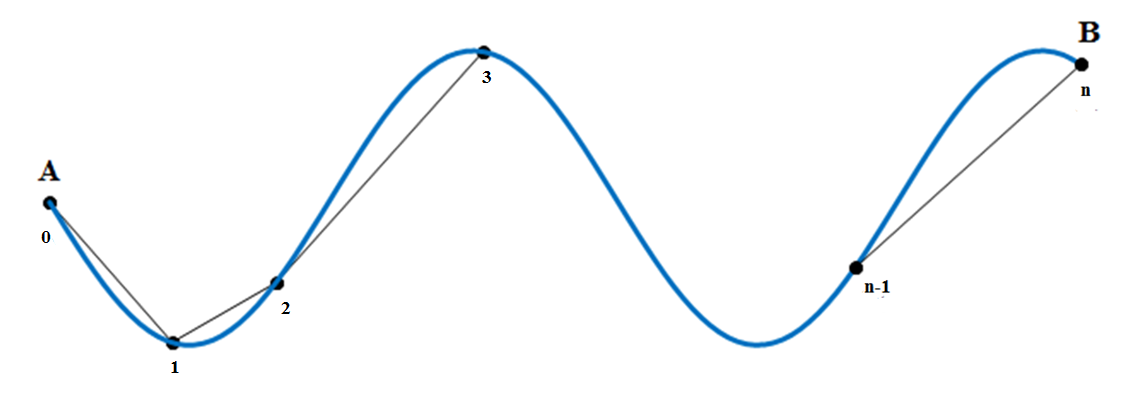
Обозначим длины звеньев этой ломаной следующим образом: длина $M_{0} M_{1} =\Delta \; l_{1} $, длина $M_{1} M_{2} =\Delta \; l_{2} $, .... , длина $M_{i-1} M_{i} =\Delta \; l_{i} $, .... , длина $M_{n-1} M_{n} =\Delta \; l_{n} $. Тогда периметр этой ломаной $l_{n} =\Delta \; l_{1} +\Delta \; l_{2} +\ldots +\Delta \; l_{i} +\ldots +\Delta \; l_{n} $ или просто $l_{n} =\sum \limits _{i=1}^{n}\Delta \; l_{i} $.
Будем уменьшать длины всех звеньев за счет увеличения их количества. При этом форма ломаной будет приближается к форме дуги кривой.
На этом основании длина дуги кривой определяется так: длиной $l$ дуги называется предел, к которому стремится периметр вписанной в эту дугу ломаной при неограниченном увеличении числа её звеньев и при стремлении к нулю наибольшей из длин её звеньев.
Соответствующее выражение имеет вид: $l=\mathop{\lim }\limits_{\max \; \Delta \; l_{i} \to 0} \sum \limits _{i=1}^{n}\Delta \; l_{i} $.
Кривые, для которых этот предел существует, называются спрямляемыми.
Формулы для длины дуги плоской кривой
Пусть кривая задана между своими точками $A$ и $B$ на отрезке $\left[a,\; b\right]$ уравнением в явном виде $y=f\left(x\right)$, где $f\left(x\right)$ -- непрерывная функция с непрерывной первой производной на этом отрезке. В этом случае длина дуги кривой между точками точками $A$ и $B$ вычисляется по формуле $l=\int \limits _{a}^{b}\sqrt{1+y'^{2} } \cdot dx $.
Найти длину дуги цепной линии $y=\frac{1}{2} \cdot \left(e^{x} +e^{-x} \right)$ на отрезке $\left[0,\; 1\right]$.
Находим производную:
\[y'=\left(\frac{1}{2} \cdot \left(e^{x} +e^{-x} \right)\right)^{{'} } =\frac{1}{2} \cdot \left(e^{x} -e^{-x} \right).\]Вычисляем:
\[1+y'^{2} =1+\left(\frac{1}{2} \cdot \left(e^{x} -e^{-x} \right)\right)^{2} =1+\frac{1}{4} \cdot \left(e^{2\cdot x} -2\cdot e^{x} \cdot e^{-x} +e^{-2\cdot x} \right)=\] \[=1+\frac{1}{4} \cdot \left(e^{2\cdot x} -2+e^{-2\cdot x} \right)=\frac{1}{4} \cdot \left(e^{x} +e^{-x} \right)^{2} ;\] \[\sqrt{1+y'^{2} } =\frac{1}{2} \cdot \left(e^{x} +e^{-x} \right).\]Находим длину дуги:
\[l=\int \limits _{a}^{b}\sqrt{1+y'^{2} } \cdot dx =\int \limits _{0}^{1}\frac{1}{2} \cdot \left(e^{x} +e^{-x} \right)\cdot dx =\frac{1}{2} \cdot \left[e^{x} -e^{-x} \right]_{0}^{1} =\] \[=\frac{1}{2} \cdot \left(\left(e^{1} -e^{-1} \right)-\left(e^{0} -e^{-0} \right)\right)=\frac{e-e^{-1} }{2} .\]Пусть кривая задана параметрическими уравнениями $x=x\left(t\right)$ и $y=y\left(t\right)$, $\alpha \le t\le \beta $. Предположим, что функции $x=x\left(t\right)$ и $y=y\left(t\right)$ и их производные непрерывны при $\alpha \le t\le \beta $, причем $x'\left(t\right)\ne 0$. В этом случае длина дуги кривой вычисляется по формуле $l=\int \limits _{\alpha }^{\beta }\sqrt{\left(x'\left(t\right)\right)^{2} +\left(y'\left(t\right)\right)^{2} } \cdot dt $.
Найти длину одной арки циклоиды $x=t-\sin t$, $y=1-\cos t$, $0\le t\le 2\cdot \pi $.
Находим производные:
\[x'=\left(t-\sin t\right)^{{'} } =1-\cos t; y'=\left(1-\cos t\right)^{{'} } =\sin t.\]Вычисляем:
\[\left(x'\right)^{2} +\left(y'\right)^{2} =\left(1-\cos t\right)^{2} +\left(\sin t\right)^{2} =2\cdot \left(1-\cos t\right)=4\cdot \sin ^{2} \frac{t}{2} .\]Находим длину дуги:
\[l=\int \limits _{0}^{2\cdot \pi }\sqrt{4\cdot \sin ^{2} \frac{t}{2} } \cdot dt =2\cdot \int \limits _{0}^{2\cdot \pi }\sin \frac{t}{2} \cdot dt =-4\cdot \left[\cos \frac{t}{2} \right]_{0}^{2\cdot \pi } =\] \[=-4\cdot \left(\cos \frac{2\cdot \pi }{2} -\cos \frac{0}{2} \right)=-4\cdot \left(-1-1\right)=8.\]Пусть кривая задана в полярных координатах $\rho =\rho \left(\phi \right)$, $\alpha \le \phi \le \beta $. Предположим, что функция $\rho =\rho \left(\phi \right)$ и её производная непрерывны при $\alpha \le \phi \le \beta $. В этом случае длина дуги кривой вычисляется по формуле $l=\int \limits _{\alpha }^{\beta }\sqrt{\rho ^{2} +\rho '^{2} } \cdot d\phi $.
Найти длину кардиоиды $\rho =1+\cos \phi $.
Так как кардиоида симметрична относительно полярной оси, то изменяя полярный угол $\phi $ от $0$ до $\pi $, мы получим половину длины кардиоиды.
Находим производную: $\rho '=-\sin \phi $.
Вычисляем:
\[\rho ^{2} +\rho '^{2} =\left(1+\cos \phi \right)^{2} +\left(-\sin \phi \right)^{2} =2\cdot \left(1+\cos \phi \right).\]Находим половину длины кардиоиды:
\[\frac{l}{2} =\int \limits _{0}^{\pi }\sqrt{2\cdot \left(1+\cos \phi \right)} \cdot d\phi =2\cdot \int \limits _{0}^{\pi }\cos \frac{\phi }{2} \cdot d\phi =4\cdot \left[\sin \frac{\phi }{2} \right]_{0}^{\pi } =4\cdot \sin \frac{\pi }{2} =4.\]Полная длина кардиоиды $l=8$.
Производная и дифференциал дуги
Пусть в формуле $l=\int \limits _{a}^{b}\sqrt{1+\left(f'\left(x\right)\right)^{2} } \cdot dx $ для длины дуги кривой, заданной в виде $y=f\left(x\right)$, $a\le x\le b$, нижняя граница интеграла $a$ остается постоянной, а верхняя граница изменяется и равна $x$.
При этом длина дуги $l\left(x\right)=\int \limits _{a}^{x}\sqrt{1+\left(f'\left(t\right)\right)^{2} } \cdot dt $ будет функцией верхней границы (переменная интегрирования переобозначена, чтобы не путать её с верхней границей).
В соответствии с теоремой о производной интеграла по верхней границе производная этой функции имеет вид $l'\left(x\right)=\sqrt{1+\left(f'\left(x\right)\right)^{2} } $.
Отсюда получаем дифференциал дуги:
$dl\left(x\right)=l'\left(x\right)\cdot dx=\sqrt{1+\left(f'\left(x\right)\right)^{2} } \cdot dx$, откуда $dl=\sqrt{1+y'^{2} } \cdot dx$ или $dl=\sqrt{dx^{2} +dy^{2} } $.
При параметрическом задании функции $x=x\left(t\right)$ и $y=y\left(t\right)$, $\alpha \le t\le \beta $ дифференциал дуги имеет вид $dl=\sqrt{\left(x'\left(t\right)\right)^{2} +\left(y'\left(t\right)\right)^{2} } \cdot dt$.
При задании функции в полярных координатах $\rho =\rho \left(\phi \right)$, $\alpha \le \phi \le \beta $ дифференциал дуги имеет вид $dl=\sqrt{\rho ^{2} +\rho '^{2} } \cdot d\phi $.

















