Способы задания кривой
Любое уравнение вида $F\left(x,y\right)=0$, связывающее декартовы прямоугольные координаты $x$ и $y$, соответствует некоторой линии (или кривой) на плоскости. Это значит, что координаты произвольной точки на линии удовлетворяют этому уравнению, и наоборот, всякая точка, координаты которой удовлетворяют уравнению, лежит на линии.
Если $F\left(x,y\right)=0$ -- многочлен, то кривая называется алгебраической, и степень многочлена называется порядком кривой. В противном случае кривая называется трансцендентной.
В декартовых прямоугольных координатах плоская кривая может быть задана не только в неявном виде $F\left(x,y\right)=0$, но и в явном $y=f\left(x\right)$, а также в параметрическом виде $x=x\left(t\right)$, $y=y\left(t\right)$. Кроме того, уравнение кривой может быть задано в полярных координатах $\rho =f\left(\phi \right)$.
Независимо от формы задания кривой, на ней всегда можно указать естественное положительное направление. Это связано, например, с возрастанием параметра $t$, если кривая задана в параметрическом виде, с возрастанием аргумента $x$, если кривая задана в явном виде, с возрастанием угла $\phi $, если кривая задана в полярных координатах.
Объекты, сопровождающие данную кривую
Основные объекты, сопровождающие данную кривую -- это локальные её элементы.
К локальным элементам кривой относятся дифференциал дуги, кривизна и радиус кривизны, круг кривизны и центр кривизны, угол между двумя кривыми, а также точки специального типа (точки перегиба, вершины, узловые точки, изолированные точки, точки возврата, точки самоприкосновения, точки излома, точки прекращения, асимптотические точки).
К другим сопровождающим объектам данной кривой относятся сопровождающие линии, свойства которых тесно связаны со свойствами данной кривой.
К сопровождающим линиям данной кривой относятся касательная к кривой, нормаль кривой, отрезки касательной и нормали, подкасательная и поднормаль кривой, асимптоты, эволюты и эвольвенты, а также огибающие семейства кривых.
Пространственные кривые
Способы задания пространственных кривых могут иметь вид координатных и векторных уравнений.
Разновидности координатных уравнений:
- пересечение двух поверхностей $F\left(x,y,z\right)=0$, $\$ \left(x,y,z\right)=0$;
- параметрические уравнения первого вида $x=x\left(t\right)$, $y=y\left(t\right)$, $z=z\left(t\right)$, где $t$ -- любой параметр, в частности $t=x$, или $t=y$, или $t=z$;
- параметрические уравнения второго вида $x=x\left(s\right)$,$y=y\left(s\right)$,$z=z\left(s\right)$, где $s$ -- длина дуги от некоторой точки $A$ до текущей точки $M$.
Векторные уравнения пространственной кривой связаны с понятием радиус-вектора точки кривой $\bar{r}$.
Вектор $\overline{OM}$, начало которого совпадает с началом координат $O$, а конец находится в точке $M$, полностью определяет эту точку и называется радиус-вектором этой точки.
Векторные уравнения кривой могут иметь следующий вид:
- $\bar{r}=\bar{r}\left(t\right)$, где $\bar{r}\left(t\right)=x\left(t\right)\cdot \bar{i}+y\left(t\right)\cdot \bar{j}+z\left(t\right)\cdot \bar{k}$;
- $\bar{r}=\bar{r}\left(s\right)$, где $\bar{r}\left(s\right)=x\left(s\right)\cdot \bar{i}+y\left(s\right)\cdot \bar{j}+z\left(s\right)\cdot \bar{k}$.
Возрастание параметра $t$ и направление отсчета длины дуги $s$естественным образом определяют положительные направления на пространственных кривых.
В каждой точке $M$ пространственной кривой (кроме некоторых особых точек) могут рассматриваться три прямые и три плоскости, взаимно пересекающиеся под прямыми углами:
- касательная прямая, которая определяется как предельное положение некоторой секущей $NM$ при условии, что точка $N$, неограниченно приближается к точке $M$; положительное направление на касательной соответствует положительному направлению на кривой; $\bar{t}$ -- единичный вектор положительного направления касательной;
- нормальная плоскость -- плоскость перпендикулярная к касательной прямой; все прямые, лежащие в этой плоскости и проходящие через точку $M$ называются нормалями к кривой в этой точке;
- соприкасающаяся плоскость -- предельное положение плоскости, проходящей через некоторые три близкие точки кривой $M$, $N$ и $P$, при условии, что точки $N$ и $P$ неограниченно приближаются к точке $M$; соприкасающаяся плоскость содержит в себе касательную прямую;
- главная нормаль -- линия пересечения нормальной и соприкасающейся плоскостей; это та из нормалей, которая лежит в соприкасающейся плоскости; на главной нормали положительное направление идет в сторону вогнутости кривой; $\bar{n}$ -- единичный вектор положительного направления нормали;
- бинормаль -- прямая, проходящая через точку $M$ перпендикулярно к соприкасающейся плоскости; положительное направление на бинормали определяется единичным вектором $\bar{b}=\bar{t}\times \bar{n}$;
- спрямляющая плоскость -- плоскость, содержащая касательную и бинормаль.
Три единичных вектора $\bar{t}$, $\bar{n}$ и $\bar{b}$ вместе с соединяющими их плоскостями образуют сопровождающий трехгранник пространственной кривой.
В точках кривой общего типа кривая расположена по одну сторону от спрямляющей плоскости и пересекает нормальную и соприкасающуюся плоскости. При этом, если спроектировать небольшой участок кривой, содержащий точку $M$, на плоскости сопровождающего трехгранника, то эти проекции приближенно будут иметь вид:
- параболы -- на соприкасающейся плоскости;
- кубической параболы -- на спрямляющей плоскости;
- полукубической параболы -- на нормальной плоскости.
Понятие кривизны плоских и пространственных кривых
Рассмотрим дугу некоторой простой кривой без особых точек.
Если в каждой её точке провести касательную, то из-за искривленности дуги эта касательная будет поворачиваться при перемещении точки касания.
Этим кривая принципиально отличается от прямой, для которой касательная не только совпадает с прямой, но и сохраняет одно и то же направление независимо от точки касания.
Важным свойством кривой является степень её искривлённости, называемая кривизной. Величину кривизны естественно характеризовать углом поворота касательной при переходе от одной точки дуги кривой к другой. При этом рассматривается относительный угол поворота, то есть угол поворота, рассчитанный на единицу длины дуги. Это отношение называют средней кривизной дуги кривой.
На различных участках различных кривых средняя кривизна различна. Например, для любой прямой средняя кривизна всегда равна нулю, для одной и той же окружности средняя кривизна везде одинакова, хотя и отличается для окружностей разных радиусов. А вот если рассмотреть среднюю кривизну для дуги синусоиды при переходе между точками, отстоящими на величину периода, то окажется, что она равна нулю, так как направление касательной в конце дуги оказывается тем же, что и в её начале.
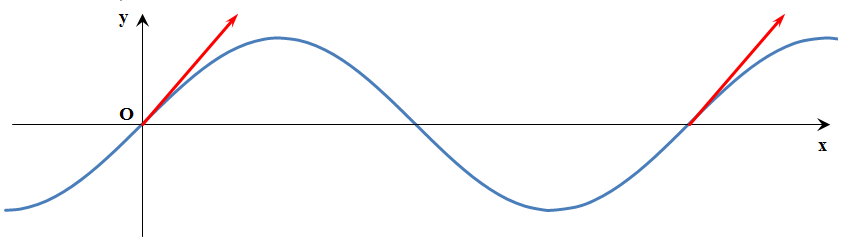
И такой результат для синусоиды не может нас устраивать, так как даже просто визуальный анализ убеждает нас в том, что искривлённость имеется.
Именно поэтому вместо средней кривизны дуги всегда рассматривают её кривизну в точке.
Кривизной дуги в некоторой её точке $M$ называется предел, к которому стремится средняя кривизна дуги $NM$ при условии, что точка $N$, неограниченно приближается вдоль кривой к точке $M$.













