Вычислить периметр плоской фигуры, ограниченной нижней частью графика параболы $y=0,75\cdot x^{2} -1,5\cdot x-2,25$, а также прямыми $11\cdot x-6\cdot y+87=0$ и $x-y+17=0$.
Строим графическое изображение фигуры:
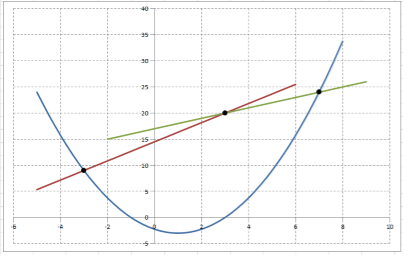
Находим точки пересечения линий, ограничивающих фигуру:
- точка пересечения прямых определяется уравнением $x+17=\frac{11\cdot x+87}{6} $, откуда $x=3$;
- точка пересечения прямой $11\cdot x-6\cdot y+87=0$ и параболы определяется уравнением $\frac{11\cdot x+87}{6} =0,75\cdot x^{2} -1,5\cdot x-2,25$, откуда получаем $9\cdot x^{2} -40\cdot x-201=0$, $x_{1} ={67\mathord{\left/ {\vphantom {67 9}} \right. } 9} $ и $x_{2} =-3$; нужным результатом является $x=-3$;
- точка пересечения прямой $x-y+17=0$ и параболы определяется уравнением $x+17=0,75\cdot x^{2} -1,5\cdot x-2,25$, откуда получаем $3\cdot x^{2} -10\cdot x-77=0$, $x_{1} =-{11\mathord{\left/ {\vphantom {11 3}} \right. } 3} $ и $x_{2} =7$; нужным результатом является $x_{2} =7$.
Известно, что если на некотором отрезке $\left[a,\; b\right]$ кривая задана уравнением $y=y\left(x\right)$, то длина её дуги вычисляется с помощью определенного интеграла (ОИ) $L=\int \limits _{a}^{b}\sqrt{1+y'^{2} \left(x\right)} \cdot dx $.
Для каждой линии вычисляем значение выражения $\sqrt{1+y'^{2} \left(x\right)} $:
- для прямой $11\cdot x-6\cdot y+87=0$ имеем $11-6\cdot y'=0$, откуда $\sqrt{1+y'^{2} \left(x\right)} =\sqrt{1+\left(\frac{11}{6} \right)^{2} } =\sqrt{\frac{157}{36} } \approx 2,09$;
- для прямой $x-y+17=0$ имеем $1-y'=0$, откуда $\sqrt{1+y'^{2} \left(x\right)} =\sqrt{1+1^{2} } =\sqrt{2} \approx 1,41$;
- для параболы $y=0,75\cdot x^{2} -1,5x-2,25$ имеем $y'=1,5\cdot x-1,5$, откуда $\sqrt{1+y'^{2} \left(x\right)} =\sqrt{1+\left(1,5\cdot x-1,5\right)^{2} } =\sqrt{2,25\cdot x^{2} -4,5\cdot x+3,25} $.
Для каждой линии определяем пределы интегрирования:
- для прямой $11\cdot x-6\cdot y+87=0$ имеем $a=-3$, $b=3$;
- для прямой $x-y+17=0$ имеем $a=3$, $b=7$;
- для параболы $y=0,75\cdot x^{2} -1,5x-2,25$ имеем $a=-3$, $b=7$.
Находим длину прямой $11\cdot x-6\cdot y+87=0$:
\[L_{1} =\int \limits _{-3}^{3}2,09\cdot dx =2,09\cdot \left[x\right]_{-3}^{3} =2,09\cdot \left(3-\left(-3\right)\right)=2,09\cdot 6\approx 12,54.\]Находим длину прямой $x-y+17=0$:
\[L_{2} =\int \limits _{3}^{7}1,41\cdot dx =1,41\cdot \left[x\right]_{3}^{7} =1,41\cdot \left(7-3\right)=1,41\cdot 4\approx 5,64.\]Находим длину параболы:
\[L_{3} =\int \limits _{-3}^{7}\sqrt{2,25\cdot x^{2} -4,5\cdot x+3,25} \cdot dx =\int \limits _{-3}^{7}\sqrt{2,25\cdot \left(x^{2} -2\cdot x+\frac{13}{9} \right)} \cdot dx =\] \[=\sqrt{2,25} \cdot \int \limits _{-3}^{7}\sqrt{x^{2} -2\cdot x+\frac{13}{9} } \cdot dx =1,5\cdot \int \limits _{-3}^{7}\sqrt{\left(x-1\right)^{2} +\frac{4}{9} } \cdot dx =\] \[=1,5\cdot \left[\frac{x-1}{2} \cdot \sqrt{\left(x-1\right)^{2} +\frac{4}{9} } +\frac{4}{18} \cdot \ln \left|x-1+\sqrt{\left(x-1\right)^{2} +\frac{4}{9} } \right|\right]_{-3}^{7} =\] \[=1,5\cdot \left(3\cdot \sqrt{36+\frac{4}{9} } +\frac{4}{18} \cdot \ln \left|6+\sqrt{36+\frac{4}{9} } \right|\right)-\] \[-1,5\cdot \left(-2\cdot \sqrt{16+\frac{4}{9} } +\frac{4}{18} \cdot \ln \left|-4+\sqrt{16+\frac{4}{9} } \right|\right)=\] \[=1,5\cdot \left(3\cdot \sqrt{36,444} +0,22\cdot \ln \left|6+\sqrt{36,444} \right|\right)-\] \[-1,5\cdot \left(-2\cdot \sqrt{16,444} +0,22\cdot \ln \left|-4+\sqrt{16,444} \right|\right)=\] \[=1,5\cdot \left(3\cdot 6,037+0,22\cdot \ln 12,037\right)-1,5\cdot \left(-2\cdot 4,055+0,22\cdot \ln 0,055\right)=\] \[=1,5\cdot \left(18,11+0,22\cdot 2,49\right)-1,5\cdot \left(-8,11+0,22\cdot \left(-2,90\right)\right)=\] \[=1,5\cdot 18,66+1,5\cdot 8,75=41,12.\]Вычисляем периметр:
\[L=L_{1} +L_{2} +L_{3} \approx 12,54+5,64+41,12\approx 59,30. \]Вычислить длину замкнутой кривой $\rho =2\cdot \sin ^{3} \frac{\phi }{3} $.
Строим графическое изображение фигуры:
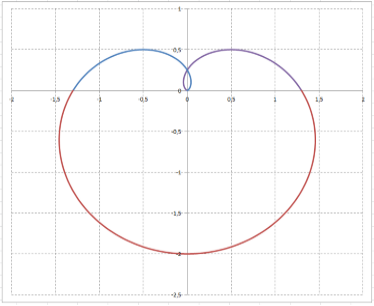
Кривая задана в полярных координатах. Цветом (синий, красный, фиолетовый) выделены три участка построения полного графика: от 0 до $\pi $, от $\pi $ до 2•$\pi $ и от 2•$\pi $ до 3•$\pi $.
Границы изменения угла $\varphi $ определяются неравенством $\rho \ge 0$. Отсюда следует: $\sin \frac{\phi }{3} \ge 0$; $0\le \frac{\phi }{3} \le \pi $; $0\le \phi \le 3\cdot \pi $.
График показывает, что при изменении угла $\phi $ от нуля до $\frac{3\cdot \pi }{2} $ длина радиус-вектора возрастает от нуля до двух. При этом конец радиус-вектора описывает левую часть дуги кривой. Когда угол $\phi $ меняется от $\frac{3\cdot \pi }{2} $ до $3\cdot \pi $, длина радиус-вектора убывает от двух до нуля. В результате получается замкнутая кривая, симметричная относительно прямой $\phi =\pm \frac{\pi }{2} $. Следовательно, для вычисления общей длины кривой можно найти половину её длины $0\le \phi \le \frac{3\cdot \pi }{2} $, после чего полученный результат удвоить.
Известно, что если на отрезке $\left[\alpha ,\; \beta \right]$ кривая задана уравнением $\rho =\rho \left(\phi \right)$ в полярной системе координат, то длина её дуги вычисляется с помощью ОИ $L=\int \limits _{\alpha }^{\beta }\sqrt{\rho ^{2} \left(\phi \right)+\rho '^{2} \left(\phi \right)} \cdot d\phi $.
Имеем: $\alpha =0$; $\beta =\frac{3\cdot \pi }{2} $; $\rho '=2\cdot \sin ^{2} \frac{\phi }{3} \cdot \cos \frac{\phi }{3} $.
Вычисляем:
\[\sqrt{\rho ^{2} +\rho '^{2} } =\sqrt{\left(2\cdot \sin ^{3} \frac{\phi }{3} \right)^{2} +\left(2\cdot \sin ^{2} \frac{\phi }{3} \cdot \cos \frac{\phi }{3} \right)^{2} } =\] \[=\sqrt{4\cdot \sin ^{6} \frac{\phi }{3} +4\cdot \sin ^{4} \frac{\phi }{3} \cdot \cos ^{2} \frac{\phi }{3} } =2\cdot \sin ^{2} \frac{\phi }{3} ;\] \[L=2\cdot \int \limits _{0}^{\frac{3\cdot \pi }{2} }2\cdot \sin ^{2} \frac{\phi }{3} \cdot d\phi =2\cdot \int \limits _{0}^{\frac{3\cdot \pi }{2} }\left(1-\cos \frac{2\cdot \phi }{3} \right)\cdot d\phi =\] \[=2\cdot \left[\phi -\frac{3}{2} \cdot \sin \frac{2\cdot \phi }{3} \right]_{0}^{\frac{3\cdot \pi }{2} } =2\cdot \frac{3\cdot \pi }{2} =3\cdot \pi .\]












