Полный перечень основных элементарных функций
К классу основных элементарных функций относятся следующие:
- Постоянная функция $y=C$, где $C$ -- константа. Такая функция принимает одно и то же значение $C$ при любом $x$.
- Степенная функция $y=x^{a} $, где показатель степени $a$ -- действительное число.
- Показательная функция $y=a^{x} $, где основание степени $a>0$, $a\ne 1$.
- Логарифмическая функция $y=\log _{a} x$, где основание логарифма $a>0$, $a\ne 1$.
- Тригонометрические функции $y=\sin x$, $y=\cos x$, $y=tg\, x$, $y=ctg\, x$, $y=\sec x$, $y=A>\sec \, x$.
- Обратные тригонометрические функции $y=\arcsin x$, $y=\arccos x$, $y=arctgx$, $y=arcctgx$, $y=arc\sec x$, $y=arc\, \cos ec\, x$.
Поведение основных элементарных функций
Степенные функции
Поведение степенной функции $y=x^{a} $ рассмотрим для тех простейших случаев, когда её показатель степени определяет целочисленные возведение в степень и извлечение корня.
Показатель степени функции $y=x^{a} $ -- натуральное число, то есть $y=x^{n} $, $n\in N$.
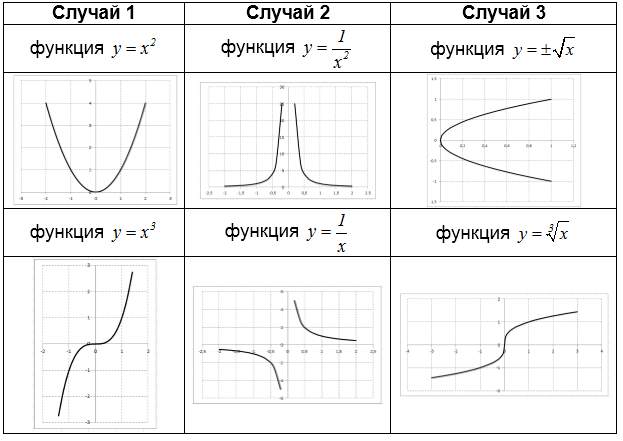
Если $n=2\cdot k$ -- четное число, то функция $y=x^{2\cdot k} $ -- четная и неограниченно возрастает как при неограниченном возрастании аргумента $\left(x\to +\infty \right)$, так и при неограниченном его убывани $\left(x\to -\infty \right)$. Такое поведение функции можно описать выражениями $\mathop{\lim }\limits_{x\to +\infty } x^{2\cdot k} =+\infty $ и $\mathop{\lim }\limits_{x\to -\infty } x^{2\cdot k} =+\infty $, которые означают, что функция в обоих случаях неограниченно возрастает ($\lim $ -- предел). Пример: график функции $y=x^{2} $.
Если $n=2\cdot k-1$ -- нечетное число, то функция $y=x^{2\cdot k-1} $ -- нечетная, неограниченно возростает при неограниченном возрастании аргумента и неограниченно убывает при неограниченном его убывании. Такое поведение функции можно описать выражениями $\mathop{\lim }\limits_{x\to +\infty } x^{2\cdot k-1} =+\infty $ и $\mathop{\lim }\limits_{x\to -\infty } x^{2\cdot k-1} =-\infty $. Пример: график функції $y=x^{3} $.
Показатель степени функци $y=x^{a} $ -- целое отрицательное число, то есть $y=\frac{1}{x^{n} } $, $n\in N$.
Если $n=2\cdot k$ -- четное число, то функция $y=\frac{1}{x^{2\cdot k} } $ -- четная и асимптотически (постепенно) приближается к нулю как при неограниченном возрастании аргумента, так и при неограниченном его убывании. Такое поведение функции можно описать единым выражением $\mathop{\lim }\limits_{x\to \infty } \frac{1}{x^{2\cdot k} } =0$, которое означает, что при неограниченном возрастании аргумента по абсолютной величине предел функции равен нулю. Кроме того, при стремлении аргумента к нулю как слева $\left(x\to 0-0\right)$, так и справа $\left(x\to 0+0\right)$, функция неограниченно возрастает. Поэтому справедливы выражения $\mathop{\lim }\limits_{x\to 0-0} \frac{1}{x^{2\cdot k} } =+\infty $ и $\mathop{\lim }\limits_{x\to 0+0} \frac{1}{x^{2\cdot k} } =+\infty $, которые означают, что функция $y=\frac{1}{x^{2\cdot k} } $ в обоих случаях имеет бесконечный предел, равный $+\infty $. Пример: график функции $y=\frac{1}{x^{2} } $.
Если $n=2\cdot k-1$ -- нечетное число, то функция $y=\frac{1}{x^{2\cdot k-1} } $ -- нечетная и асимптотически приближается к нулю как при неограниченном возрастании аргумента, так и при неограниченном его убывании. Такое поведение функции можно описать единым выражением $\mathop{\lim }\limits_{x\to \infty } \frac{1}{x^{2\cdot k-1} } =0$. Кроме того, при приближении аргумента к нулю слева функция неограниченно убывает, а при приближении аргумента к нулю справа функция неограниченно возрастает, то есть $\mathop{\lim }\limits_{x\to 0-0} \frac{1}{x^{2\cdot k-1} } =-\infty $ и $\mathop{\lim }\limits_{x\to 0+0} \frac{1}{x^{2\cdot k-1} } =+\infty $. Пример: график функции $y=\frac{1}{x} $.
Показатель степени функции $y=x^{a} $ -- число, обратное к натуральному, то есть $y=\sqrt[{n}]{x} $, $n\in N$.
Если $n=2\cdot k$ -- четное число, то функция $y=\pm \sqrt[{2\cdot k}]{x} $ является двузначной и определена только при $x\ge 0$. При неограниченном возрастании аргумента значение функции $y=+\sqrt[{2\cdot k}]{x} $ неограниченно возрастает, а значение функции $y=-\sqrt[{2\cdot k}]{x} $ неограниченно убывает, то есть $\mathop{\lim }\limits_{x\to +\infty } \left(+\sqrt[{2\cdot k}]{x} \right)=+\infty $ и $\mathop{\lim }\limits_{x\to +\infty } \left(-\sqrt[{2\cdot k}]{x} \right)=-\infty $. Пример: график функции $y=\pm \sqrt{x} $.
Если $n=2\cdot k-1$ -- нечетное число, то функция $y=\sqrt[{2\cdot k-1}]{x} $ -- нечетная, неограниченно возрастает при неограниченном возрастании аргумента и неограниченно убывает при неограниченном его убывает, то есть $\mathop{\lim }\limits_{x\to +\infty } \sqrt[{2\cdot k-1}]{x} =+\infty $ и $\mathop{\lim }\limits_{x\to -\infty } \sqrt[{2\cdot k-1}]{x} =-\infty $. Пример: график функции $y=\sqrt[{3}]{x} $.
Показательная и логарифмическая функции
Показательная $y=a^{x} $ и логарифмическая $y=\log _{a} x$ функции являются взаимно обратными. Их графики симметричны относительно общей биссектрисы первого и третьего координатных углов.
При неограниченном возрастании аргумента $\left(x\to +\infty \right)$ показательная функция или неограниченно возрастает $\mathop{\lim }\limits_{x\to +\infty } a^{x} =+\infty $, если $a>1$, или асимптотически приближается к нулю $\mathop{\lim }\limits_{x\to +\infty } a^{x} =0$, если $a1$, или неограниченно возрастает $\mathop{\lim }\limits_{x\to -\infty } a^{x} =+\infty $, если $a
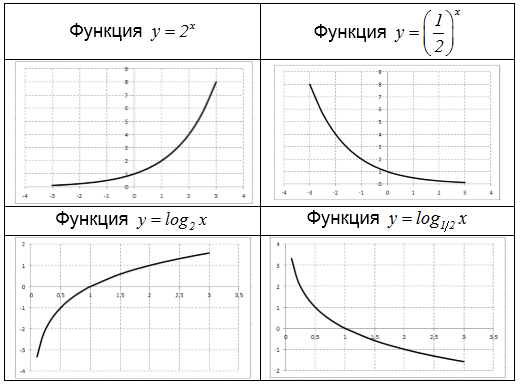
Характерным значением для функции $y=a^{x} $ является значение $x=0$. При этом все показательные функции, независимо от $a$, обязательно пересекают ось $Oy$ при $y=1$. Примеры: графики функций $y=2^{x} $ и $y = \left (\frac{1}{2} \right)^{x} $.
Логарифмическая функция $y=\log _{a} x$ определена только при $x > 0$.
При неограниченном возрастании аргумента $\left(x\to +\infty \right)$ логарифмическая функция или неограниченно возрастает $\mathop{\lim }\limits_{x\to +\infty } \log _{a} x=+\infty $, если $a>1$, или неограниченно убывает $\mathop{\lim }\limits_{x\to +\infty } \log _{a} x=-\infty $, если $a1$, или неограниченно возрастает $\mathop{\lim }\limits_{x\to 0+0} \log _{a} x=+\infty $, если $a
Характерным значением для функции $y=\log _{a} x$ является значение $y=0$. При этом все логарифмические функции, независимо от $a$, обязательно пересекают ось $Ox$ при $x=1$. Примеры: графики функций $y=\log _{2} x$ и $y=\log _{1/2} x$.
Некоторые логарифмические функции имеют специальные обозначения. В частности, если основание логарифма $a=10$, то такой логарифм называется десятичным, а соответствующая функция записывается как $y=\lg x$. А если основанием логарифма выбирается иррациональное число $e=2,7182818\ldots $, то такой логарифм называется натуральным, а соответствующая функция записывается как $y=\ln x$. Обратной к ней является функция $y=e^{x} $, называемая экспонентой.











