Арксинус
Рассмотрим на множестве $X=\left[-\frac{\pi }{2},\frac{\pi }{2}\right]$ функцию $y=sinx$. Она непрерывна и возрастает на множестве $X$ и отображает множество $X=\left[-\frac{\pi }{2},\frac{\pi }{2}\right]$ на множество $Y=[-1,1]$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=sinx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=[-1,1]$ и отображает множество $[-1,1]$ на множество $\left[-\frac{\pi }{2},\frac{\pi }{2}\right]$. Эта обратная функция называется арксинусом и обозначается $x=arcsiny$.
В более привычной для нас записи имеем $y=arcsinx$. График функции арксинуса изображен на рисунке 1.
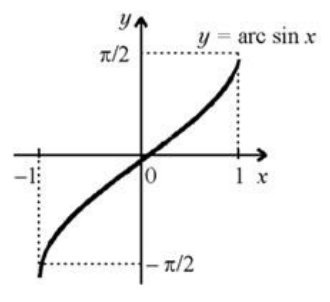
Рисунок 1. График функции арксинуса.
Арккосинус
Рассмотрим на множестве $X=\left[0,\pi \right]$ функцию $y=cosx$. Она непрерывна и убывает на множестве $X$ и отображает множество $X=\left[0,\pi \right]$ на множество $Y=[-1,1]$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=cosx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=[-1,1]$ и отображает множество $[-1,1]$ на множество $\left[0,\pi \right]$. Эта обратная функция называется арккосинусом и обозначается $x=arccosy$.
В более привычной для нас записи имеем $y=arccosx$. График функции арккосинуса изображен на рисунке 2.
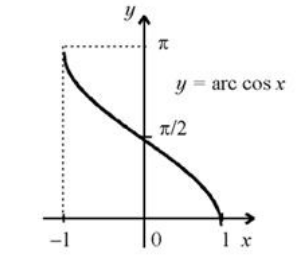
Рисунок 2. График функции арккосинуса.
Арктангенс
Рассмотрим на множестве $X=\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ функцию $y=tgx$. Она непрерывна и возрастает на множестве $X$ и отображает множество $X=\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ на множество $Y=R$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=tgx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=R$ и отображает множество $R$ на множество $\left(-\frac{\eth }{2},\frac{\pi }{2}\right)$. Эта обратная функция называется арктангенсом и обозначается $x=arctgy$.
В более привычной для нас записи имеем $y=arctgx$. График функции арктангенса изображен на рисунке 3.
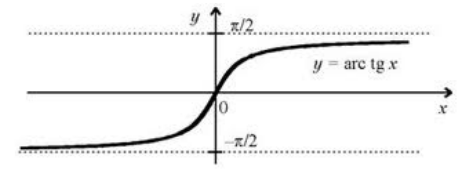
Рисунок 3. График функции арктангенса.
Арккотангенс
Рассмотрим на множестве $X=(0,\pi )$ функцию $y=ctgx$. Она непрерывна и убывает на множестве $X$ и отображает множество $X=(0,\pi )$ на множество $Y=R$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=ctgx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=R$ и отображает множество $R$ на множество $(0,\pi )$. Эта обратная функция называется арккосинусом и обозначается $x=arcctgy$.
В более привычной для нас записи имеем $y=arcctgx$. График функции арккотангенса изображен на рисунке 4.
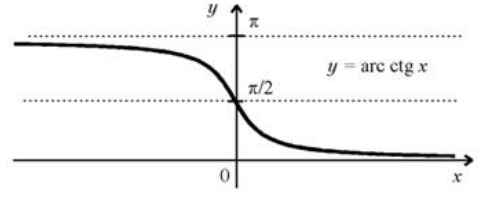
Рисунок 4. График функции арккосинуса.
Таблица значений обратных тригонометрических функций
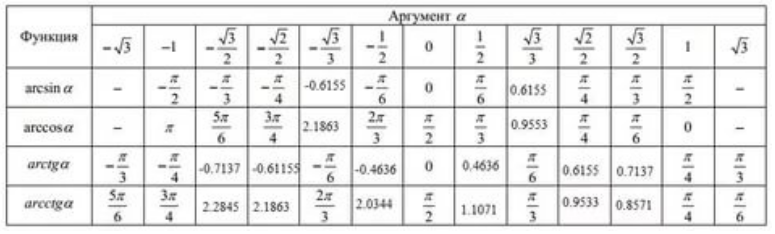
Рисунок 5.
Используя график функции $y=arcsinx$ запишем основные свойства данной функции.
- Область определения $\left[-1,1\right]$.
- Область значения $\left[-\frac{\pi }{2},\frac{\pi }{2}\right]$.
- Функция нечетна.
- Функция непериодическая.
- Функция проходит через начало координат.
- Функция выше оси $Ox$ при $x\in (0,1]$.
- Функция ниже оси $Ox$ при $x\in [-1,0)$.
- Функция возрастает на всей области определения.
- Функция непрерывна на всей области определения.
Исследование остальных трех обратных тригонометрических функций предоставляем читателю.












