Формулы приведения
Формулы приведения дают возможность находить значения тригонометрических функций для любых углов (а не только острых). С их помощью можно совершать преобразования, упрощающие вид тригонометрических выражений.
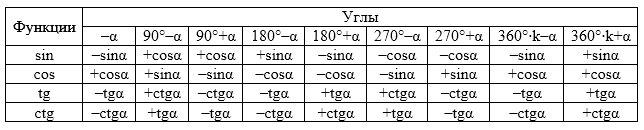
Рисунок 1.
Кроме формул приведения при решении задач используются следующие основные формулы.
1) Формулы одного угла:
2) Выражение одних тригонометрических функций через другие:
В этих формулах перед знаком радикала должен быть поставлен знак $"+"$ или $"-"$ в зависимости от того, в какой четверти находится угол.
Сумма и разность синусов, сумма и разность косинусов
Формулы суммы и разности функций:
Кроме формул суммы и разности функций, при решении задач бывают полезны формулы произведения функций:
Основные соотношения между элементами косоугольных треугольников
Обозначения:
$a$, $b$, $c$ - стороны треугольника;
$A$, $B$, $C$ - противолежащие перечисленным сторонам углы;
$p=\frac{a+b+c}{2} $ - полупериметр;
$S$ - площадь;
$R$ - радиус описанной окружности;
$r$ - радиус вписанной окружности.
Основные соотношения:
1) $\frac{a}{\sin A} =\frac{b}{\sin B} =\frac{c}{\sin C} =2\cdot R$ - теорема синусов;
2) $a^{2} =b^{2} +c^{2} -2\cdot b\cdot c\cdot \cos A$ - теорема косинусов;
3) $\frac{a+b}{a-b} =\frac{tg\frac{A+B}{2} }{tg\frac{A-B}{2} } $ - теорема тангенсов;
4) $S=\frac{1}{2} \cdot a\cdot b\cdot \sin C=\sqrt{p\cdot \left(p-a\right)\cdot \left(p-b\right)\cdot \left(p-c\right)} =r\cdot p=\frac{a\cdot b\cdot c}{4\cdot R} $ - формулы площади.
Решение косоугольных треугольников
Решение косоугольных треугольников предполагает определение всех его элементов: сторон и углов.
Даны три стороны $a$, $b$, $c$:
1) в треугольнике для вычисления углов можно применять только теорему косинусов, так как только главное значение арккосинуса находится в пределах $0\le \arccos x\le +\pi $, соответствующих треугольнику;
2) находим угол $A$, применив теорему косинусов $\cos A=\frac{b^{2} +c^{2} -a^{2} }{2\cdot b\cdot c} $, а затем обратную тригонометрическую функцию $A=\arccos \left(\cos A\right)$;
3) находим угол $B$, применив теорему косинусов $\cos B=\frac{a^{2} +c^{2} -b^{2} }{2\cdot a\cdot c} $, а затем обратную тригонометрическую функцию $B=\arccos \left(\cos B\right)$;
4) находим угол $C$ по формуле $C=180{}^\circ -\left(A+B\right)$.
Даны две стороны $a$, $b$ и угол $C$ между ними:
1) находим сторону $c$ по теореме косинусов $c^{2} =a^{2} +b^{2} -2\cdot a\cdot b\cdot \cos C$;
2) находим угол $A$, применив теорему косинусов $\cos A=\frac{b^{2} +c^{2} -a^{2} }{2\cdot b\cdot c} $, а затем обратную тригонометрическую функцию $A=\arccos \left(\cos A\right)$;
3) находим угол $B$ по формуле $B=180{}^\circ -\left(A+C\right)$.
Даны два угла $A$, $B$ и сторона $c$:
1) находим угол $C$ по формуле $C=180{}^\circ -\left(A+B\right)$;
2) находим сторону $a$ по теореме синусов $a=\frac{c\cdot \sin A}{\sin C} $;
3) находим сторону $b$ по теореме синусов $b=\frac{c\cdot \sin B}{\sin C} $.
Даны стороны $a$, $b$ и угол $B$, противолежащий стороне $b$:
1) записываем теорему косинусов $b^{2} =a^{2} +c^{2} -2\cdot a\cdot c\cdot \cos B$, используя заданные величины; отсюда получаем квадратное уравнение $c^{2} -\left(2\cdot a\cdot \cos B\right)\cdot c+\left(a^{2} -b^{2} \right)=0$ относительно стороны $c$;
2) решив полученное квадратное уравнение, теоретически можем получить один из трех случаев -- два положительных значения для стороны $c$, одно положительное значение для стороны $c$, отсутствие положительных значений для стороны $c$; соответственно и задача будет иметь два, одно или нуль решений;
3) используя конкретное положительное значение стороны $c$, находим угол $A$, применив теорему косинусов $\cos A=\frac{b^{2} +c^{2} -a^{2} }{2\cdot b\cdot c} $, а затем обратную тригонометрическую функцию $A=\arccos \left(\cos A\right)$;
4) находим угол $C$ по формуле $C=180{}^\circ -\left(A+B\right)$.













