Тригонометрические формулы
Тригонометрические формулы основаны на тригонометрических функциях (ТФ) углов.
Угол - есть фигура, образованная двумя двумя лучами $OA$ и $OB$ (стороны угла), исходящими из одной точки $O$ (вершина угла).
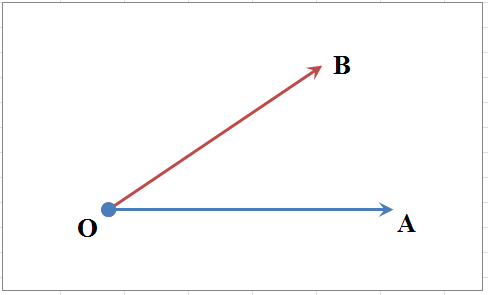
Рисунок 1.
Мерой угла служит величина поворота вокруг вершины $O$, переводящего луч $OA$ в положение $OB$.
Распространены две системы измерения углов: градусная и радианная.
В градусной системе измерения углов за единицу принимается поворот луча на $1/360$ часть одного полного оборота -- градус (обозначение ${}^\circ $). Полный оборот составляет, таким образом, $360{}^\circ $. Градус делится на 60 минут (обозначение $'$); минута -- на 60 секунд (обозначение $''$).
В радианной системе измерения углов за единицу измерения принимается острый угол ($MON$), под которым видна из центра окружности её дуга $MN$, равная радиусу ($\mathop{MN}\limits^{\cup } =OM$). Такой угол называется радианом.
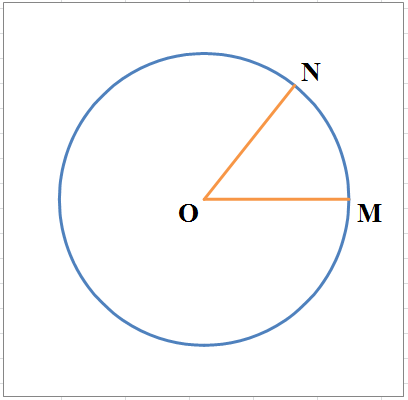
Рисунок 2.
Теперь допустим, что угол $MON$ -- произвольный. Тогда радианная мера этого угла равна отношению длины дуги $\mathop{MN}\limits^{\cup } $, описанной произвольным радиусом из центра $O$ и заключенной между сторонами угла, к радиусу $OM$ этой дуги.
Мера угла считается положительной, если вращение луча (радиуса $OM$) совершается против часовой стрелки, и отрицательной -- в противном случае.
Переход от одного измерения к другому осуществляется по формулам: $\alpha {}^\circ =\frac{180}{\pi } \cdot \alpha$ или $\alpha =\frac{\pi }{180} \cdot \alpha {}^\circ $.
Полезно помнить следующую таблицу градусной и радианной меры некоторых часто встречающихся углов:
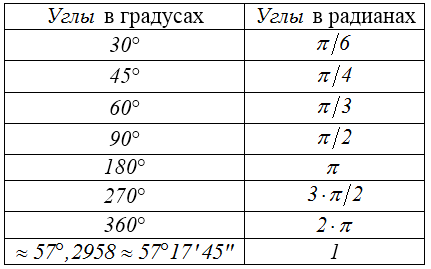
Рисунок 3.
Определение синуса, косинуса и тангенса, знаки синуса, косинуса и тангенса
ТФ острого угла можно определить из прямоугольного треугольника:
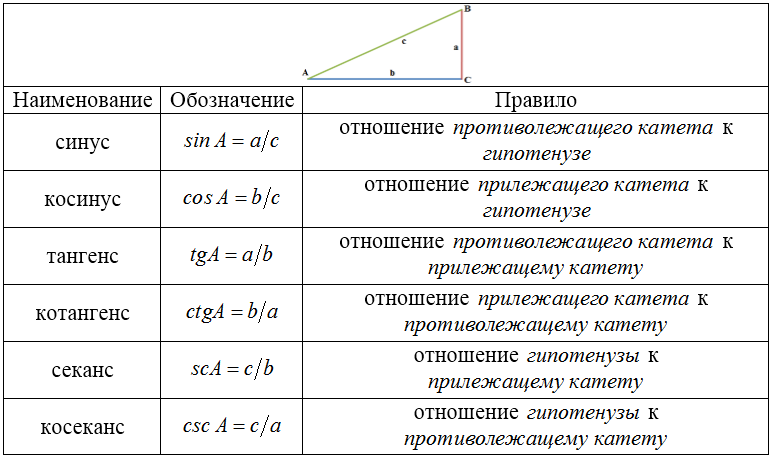
Рисунок 4.
Из этой таблицы видно, как через синус и косинус можно выразить все остальные функции: $tgA=\frac{\sin A}{\cos A} $; $ctgA=\frac{\cos A}{\sin A} $; $scA=\frac{1}{\cos A} $; $\csc A=\frac{1}{\sin A} $.
Полезно помнить значения основных ТФ для часто встречающихся значений углов:
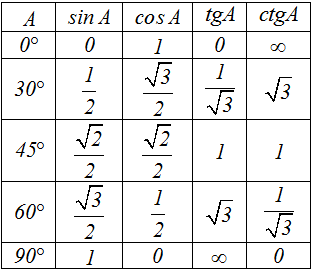
Рисунок 5.
ТФ приписывается определенный знак в зависимости от того, в какой четверти тригонометрического круга лежит подвижный радиус $OC$, образующий угол с неподвижным радиусом $OA$:

Рисунок 6.
Обратные тригонометрические функции (ОТФ)
ОТФ называются угловые величины $y$ (в радианах), определяемые следующими равенствами и указываемые с прописной буквы:
$y=Arc\sin x$, если $x=\sin y$ -- арксинус;
$y=Arc\cos x$, если $x=\cos y$ -- арккосинус;
$y=Arctgx$, если $x=tgy$ -- арктангенс;
$y=Arcctgx$, если $x=ctgy$ -- арккотангенс.
ОТФ многозначны. Поэтому из всего множества значений каждой из них выделяют главные, а наименования указывают со строчной буквы:
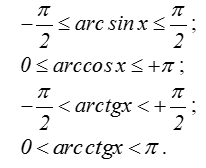
Рисунок 7.
$arc\sin \frac{\sqrt{3} }{2} =\frac{\pi }{3} $, так как $\sin \frac{\pi }{3} =\frac{\sqrt{3} }{2} $ и $\frac{\pi }{3} \in \left[-\frac{\pi }{2} ;\; \frac{\pi }{2} \right]$.
$\arccos \left(-\frac{1}{2} \right)=\frac{2\cdot \pi }{3} $, так как $\cos \frac{2\cdot \pi }{3} =-\frac{1}{2} $ и $\frac{2\cdot \pi }{3} \in \left[0;\; \pi \right]$.
$arctg1=\frac{\pi }{4} $, так как $tg\frac{\pi }{4} =1$ и $\frac{\pi }{4} \in \left(-\frac{\pi }{2} ;\; \frac{\pi }{2} \right)$.
$arcctg\sqrt{3} =\frac{\pi }{6} $, так как $ctg\frac{\pi }{6} =\sqrt{3} $ и $\frac{\pi }{6} \in \left(0;\; \pi \right)$.
Связь между значениями ОТФ и их главными значениями представляется следующими формулами:














