Понятие прямоугольного треугольника
Вначале рассмотрим понятие произвольного треугольника.
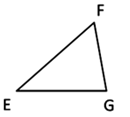
Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками (рис. 1).
Точки в рамках определения 1 будем называть вершинами треугольника.
Отрезки в рамках определения 1 будем называть сторонами треугольника.
Очевидно, что любой треугольник будет иметь 3 вершин, а также три стороны.
Теперь введем, непосредственно, понятие прямоугольного треугольника.
Треугольник будем называть прямоугольным, если один из его углов равняется $90^\circ$.
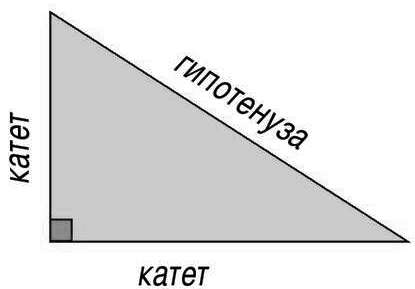
При этом стороны, которые прилегают к прямому углу, будут называться катетами, а третья сторона – гипотенузой (рис. 2).
Как и для любого треугольника, для прямоугольного справедлива следующая теорема:
Сумма углов в любом произвольном треугольнике равняется $180^\circ$.
Свойства прямоугольного треугольника
Сформулируем в виде теорем основные свойства для прямоугольных треугольников.
Острые углы в произвольном прямоугольном треугольнике в сумме дают $90^\circ$.
Доказательство.
Обозначим острые углы треугольника через $α$ и $β$. Тогда, так как наш треугольник прямоугольный, то, по теореме 1, получим
$α+β+90^\circ=180^\circ$
$α+β=90^\circ$
Теорема доказана.
Если катет в прямоугольном треугольнике находится напротив острого угла, равного $30^\circ$, то такой катет будет равняться половине гипотенузы.
Доказательство.
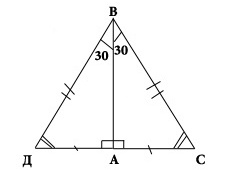
Пусть нам дан прямоугольный треугольник $DAB$, в котором $∠A=90^\circ$, а $∠B=30^\circ$. Достроим к нему треугольник $ABC$, который будет равен треугольнику $DAB$ (рис. 3).
Так как $∠A=90^\circ$, а $∠B=30^\circ$, то, по теореме 1, получим
$∠D=180^\circ-90^\circ-30^\circ=60^\circ$
Аналогично, $∠C=60^\circ$.
Также видим, что $∠B=∠DBA+∠CBA=30^\circ+30^\circ=60^\circ$.
Получаем, что треугольник $DBC$ равносторонний, следовательно, $DC=AB$. Значит, так как $DA=AC$, то $DA=\frac{1}{2} AB$.
Теорема доказана.
Справедлива также и обратная теорема:
Если катет в прямоугольном треугольнике будет равняться половине гипотенузы, то угол, который находится напротив него, равняется $30^\circ$.
Доказательство.
Пусть нам дан прямоугольный треугольник $DAB$, в котором $∠A=90^\circ$ и $DA=\frac{1}{2} AB$. Достроим к нему треугольник $ABC$, который будет равен треугольнику $DAB$ как на рисунке 3.
Так как $DA=\frac{1}{2} AB$, а $DA=AC$, то получим, что $DC=DB=CB$.
Получаем, что треугольник $DBC$ равносторонний, следовательно, все углы в нем равняются по $60^\circ$. Значит, в исходном треугольнике, $∠B=30^\circ$.
Теорема доказана.
Признаки прямоугольных треугольников
Введем теперь теоремы, которые называются признаками прямоугольного треугольника. В рамках этой статьи их доказательства рассматривать не будем.
Если катеты двух прямоугольных треугольников попарно равны, то и эти треугольники равны.
Если один из катетов прямоугольного треугольника, а также острый угол к нему прилегающий равняются одному катету и острому углу, к нему прилегающего другого прямоугольного треугольника, то и эти треугольники будут равными.
Если гипотенуза прямоугольного треугольника, а также его острый угол равняются гипотенузе и острому углу другого прямоугольного треугольника, то и эти треугольники будут равными.
Если гипотенуза прямоугольного треугольника, а также его катет равняются гипотенузе и катету другого прямоугольного треугольника, то и эти треугольники будут равными.
Пример задачи
Найти периметр равностороннего треугольника, если его высота равняется $13 см$.
Решение.
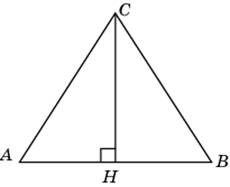
Изобразим рисунок по условию задачи:
Так как в равнобедренном треугольнике (каким является и равносторонний) высота также является медианой, то $AH=HB$.
Так как в равнобедренном треугольнике высота также является биссектрисой, то $∠ACH=30^\circ$.
По теореме 3, получим, что
$AH=\frac{1}{2} CH=6,5$
$P=AC+CB+HB+AH=6AH=39$
Ответ: $39$.