Теорема Пифагора

Источник статьи

Автор24 — учеба по твоим правилам

Предварительные сведения

Для начала введем сведения и обозначения, которые будут необходимы нам в дальнейшем.

Будем рассматривать прямоугольный треугольник $ABC$ с длинами катетов, равными $BC=a$ и $AC=b$ и длиной гипотенузы, равной $AB=c$ (рис. 1).

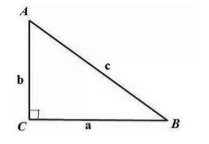
Рисунок 1.

Введем без доказательств теоремы о площади квадрата и треугольника.

Теорема 1

Площадь квадрата определяется как квадрат длины его стороны, то есть

$S=a^2$

Теорема 2

Площадь треугольника определяется как половина произведения длины его стороны, на высоту, проведенную к ней, то есть

$S=\frac{1}{2}ah$

Теорема Пифагора

Теперь введем и докажем теорему, которая носит название теоремы Пифагора.

Теорема 3

Сумма квадратов катетов прямоугольного треугольника равняется квадрату гипотенузы этого треугольника.

Математически это можно записать следующим образом:

$a^2+b^2=c^2$

Доказательство.

Пусть нам дан прямоугольный треугольник с обозначениями, как на рисунке 1. Достроим его до квадрата со стороной, равной $a+b$ (рис. 2).

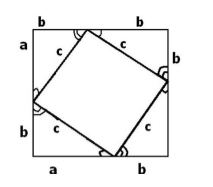
Рисунок 2.

Этот квадрат состоит из четырех равных исходному прямоугольных треугольника и квадрата, со стороной $c$ .

Площадь $S$ этого квадрата, по теореме 1, равняется

$S={(a+b)}^2=a^2+2ab+b^2$

а площадь $S''$ «малого» квадрата равняется

$S''=c^2$

По теореме 2, площадь прямоугольного треугольника $S'$ равняется

$S'=\frac{1}{2}ab$

По основному свойству площади многоугольника получим

$S=S^{''}+4S'$

$a^2+2ab+b^2=c^2+2ab$

$a^2+b^2=c^2$

Теорема доказана.

«Теорема Пифагора» 👇

Помощь эксперта по теме работы

Найти эксперта

Решение задач от ИИ за 2 минуты

Решить задачу

Помощь с рефератом от нейросети

Написать ИИ

Теорема, обратная теореме Пифагора

Теорема 4

Если в произвольном треугольнике со сторонами $a,\ b,\ c$ (где $c$ - большая сторона) выполняется равенство

$a^2+b^2=c^2$

то этот треугольник будет прямоугольным.

Доказательство.

Пусть нам дан прямоугольный треугольник с обозначениями, как на рисунке 1. Построим прямоугольный треугольник $A'B'C'$ с прямым углом $C$ так, что $A'C'=AC,\ B'C'=BC$ . Применяя теорему Пифагора, получим

${(A'B')}^2={(A'C')}^2+{(B'C')}^2$

${(A'B')}^2=a^2+b^2$

Следовательно, ${(A'B')}^2={AB}^2,\ \ значит\ AB=A'B'$ .

По $III$ признаку равенства треугольников

$\triangle ABC=\triangle A'B'C'$

Значит, угол $C$ прямой и треугольник $ABC$ прямоугольный.

Теорема доказана.

Примеры задач

Пример 1

Найти основание равнобедренного прямоугольного треугольника, если его боковая сторона равняется $8$ см.

Решение.

Обозначим основание треугольника через $x$ .

Так как треугольник является прямоугольным, то для нахождения основания воспользуемся теоремой Пифагора (теорема 3). Получим

$x^2=8^2+8^2$

$x^2=64+64$

$x^2=128$

$x=\sqrt{128}=8\sqrt{2}$

Ответ: $8\sqrt{2}$ .

Пример 2

Дан треугольник со следующими сторонами:

а) $5, 12, 13$ .

б) $6, 5, 4$ .

в) $3, 4, 5$ .

Найти среди них прямоугольные.

Решение.

Для решения будем пользоваться теоремой. Обратной теореме Пифагора (теорема 4), подставляя значения в равенство $a^2+b^2=c^2$ и проверяя его истинность.

а) Подставляя, получим

${13}^2={12}^2+5^2$

$169=169-верно$

Значит, треугольник является прямоугольным.

б) Подставляя, получим

$6^2=4^2+5^2$

$36=41-неверно$

Значит, треугольник не является прямоугольным.

в) Подставляя, получим

$5^2=4^2+3^2$

$25=25-верно$

Значит, треугольник является прямоугольным.

Замечание 1

Отметим, что прямоугольные треугольники с целыми значениями длин сторон называются пифагоровыми (пример -- пункт а), а со значениями сторон $3$ , $4$ и $5$ -- египетским (пример -- пункт в).