Площадь многоугольника
Понятие площади многоугольника будем связывать с такой геометрической фигурой, как квадрат. За единицу площади многоугольника будем принимать площадь квадрата со стороной, равной единице. Введем два основных свойства, для понятия площади многоугольника.
Свойство 1: Для равных многоугольников значения их площадей равны.
Свойство 2: Любой многоугольник можно разбить на несколько многоугольников. При этом площадь исходного многоугольника равняется сумме площадей всех многоугольников, на которые разбит данный многоугольник.
Далее рассмотрим вывод формул для площадей квадрата и прямоугольника.
Площадь квадрата
Площадь квадрата определяется как квадрат длины его стороны.
Математически это можно записать следующим образом
\[S=a^2\]где $a$ -- длина стороны квадрата.
Доказательство.
Для доказательства нам необходимо рассмотреть три случая.
-
Пусть $a=\frac{1}{n},\ n\in {\mathbb N}$.
Рассмотрим квадрат, длина стороны которого равна единице и разобьем его на $n^2$ равных между собой квадратов (рис.1).
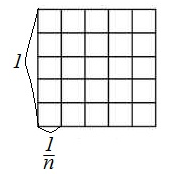
Рисунок 1.Площадь всего квадрата. По введенному понятию площади, равняется единице, следовательно, по свойству площадей 2, площадь маленького квадрата равняется
\[S=\frac{1}{n^2}=a^2\] -
Пусть $a$ десятичная дробь, имеющая $n$ знаков после запятой.
Пусть $m=a\cdot {10}^n$. Число $m\in {\mathbb N}$. Рассмотрим квадрат, длина стороны которого равна $a$ и разобьем его на $m^2$ равных между собой квадратов(рис. 2). Каждая сторона маленького квадрата равняется
\[\frac{a}{m}=\frac{a}{a\cdot {10}^n}=\frac{1}{{10}^n}\]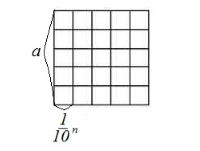
Рисунок 2.Тогда по свойству $1$ и пункту $1$ данного доказательства, имеем
\[S=m^2{\left(\frac{1}{{10}^n}\right)}^2={\left(\frac{a\cdot {10}^n}{{10}^n}\right)}^2=a^2\] -
Пусть $a$ -- бесконечная десятичная дробь.
Построим число $b$ отбросив от числа $a$ десятичных знаков после запятой, начиная с $\left(n+1\right)$ десятичного знака. Для чисел $a$ и $b$ выполняется неравенство
\[b\le a\le b+\frac{1}{{10}^n}\]то есть
\[b^2\le a^2\le {\left(b+\frac{1}{{10}^n}\right)}^2\]Для искомой площади также выполняется следующее неравенство
\[b^2\le S\le {\left(b+\frac{1}{{10}^n}\right)}^2\]Так как, при $n\to \infty $
\[{\mathop{\lim }_{n\to \infty } {\left(b+\frac{1}{{10}^n}\right)}^2\ }=b^2\]то из двух последних неравенств, получим
\[S=a^2\]
Теорема доказана.
Площадь прямоугольника
Площадь прямоугольника определяется произведением длин его смежных сторон.
Математически это можно записать следующим образом
\[S=ab\]Доказательство.
Пусть нам дан прямоугольник $ABCD$, у которого $AB=b,\ AD=a$. Достроим его до квадрата $APRV$, длина стороны которого равняется $a+b$ (рис. 3).
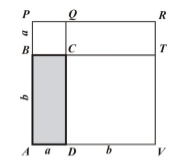
Рисунок 3.
По второму свойству площадей имеем
\[S_{ABCD}+S_{CQRT}+S_{BPQC}+S_{DCTV}=S_{APRV}\] \[2S_{ABCD}=S_{APRV}-S_{BPQC}-S_{DCTV}\] \[S_{ABCD}=\frac{S_{APRV}-S_{BPQC}-S_{DCTV}}{2}\]По теореме 1
\[S_{APRV}={(a+b)}^2,\ S_{BPQC}=a^2,\ S_{DCTV}=b^2\] \[S_{ABCD}=\frac{a^2+2ab+b^2-a^2-b^2}{2}=ab\]Теорема доказана.
Пример задач
Найти площадь прямоугольника со сторонами $5$ и $3$.
Решение.
По теореме $2$, получим
\[S=5\cdot 3=15\]Ответ: $15.$
Найти площадь квадрата, диагональ которого равняется $10$.
Решение.
Обозначим сторону квадрата через $a$. Тогда, по теореме Пифагора
\[a^2+a^2=100\] \[{2a}^2=100\] \[a^2=50\] \[a=5\sqrt{2}\]По теореме $1$
\[S={\left(5\sqrt{2}\right)}^2=50\]Ответ: $50.$


















