Понятие четырехугольника
Введем для начала понятие многоугольника вообще.
Многоугольником называется геометрическая фигура в плоскости, которая состоит из попарно соединенных между собой отрезков, соседние из которых не лежат на одной прямой.
При этом отрезки называются сторонами многоугольника, а их концы -- вершинами многоугольника.
Четырехугольником называется многоугольник, у которого $4$ вершины.
Четырехугольники могут быть выпуклыми и невыпуклыми.
Если четырехугольник всегда будет лежать по одну сторону от любой прямой, проходящей через его стороны, то он называется выпуклым (рис. 1).
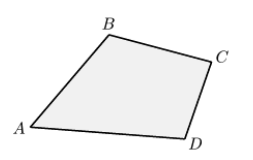
Рисунок 1. Выпуклый четырехугольник
Если четырехугольник лежит по разные стороны хотя бы одной прямой, проходящей через его стороны, то он называется невыпуклым (рис. 2).
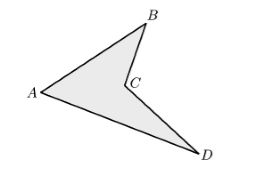
Рисунок 2. Невыпуклый четырехугольник
Классическими примерами выпуклых четырехугольников являются квадрат, прямоугольник, трапеция, ромб, параллелограмм. Рассмотрим далее эти фигуры по отдельности.
Параллелограмм
Параллелограмм -- это четырехугольник, в котором противоположные стороны параллельны между собой (рис. 3).
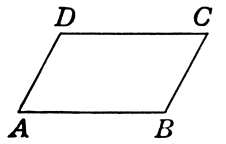
Рисунок 3. Параллелограмм
Трапеция
Трапеция -- это четырехугольник, в котором две противоположные стороны параллельны между собой, а другие две противоположные стороны не параллельны между собой (рис. 4).
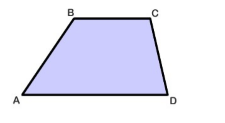
Рисунок 4. Трапеция
Квадрат
Прямоугольник, у которого все его четыре стороны равны между собой, называется квадратом (рис. 5).
Рисунок 5. Квадрат
Прямоугольник
Параллелограмм, у которого есть прямой угол, называется прямоугольником (рис. 6).

Рисунок 6. Прямоугольник
Ромб
Параллелограмм, у которого все его четыре стороны равны между собой, называется ромбом (рис. 7).
Рисунок 7. Ромб
Пример задачи
Найти площадь ромба, диагонали которого равняются $8$ см и $6$ см.
Решение.
Рассмотрим ромб $ABCD$, диагонали которого пересекаются в точке $O$ (рис. 8).
Найдем его площадь по следующей формуле $S=a^2sin\alpha $.
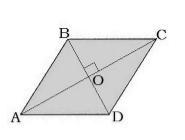
Рисунок 8.
Так как диагонали ромб делятся пополам их точкой пересечения и перпендикулярны друг другу и являются биссектриссами, то $\triangle ABO$ -- прямоугольный с катетами, равными $3$ см и $4$ см. По теореме Пифагора
\[a^2=9+16\] \[a^2=25\] \[a=5\]По определениям синуса и косинуса, имеем
\[sinBAO=\frac{BO}{AB}=\frac{3}{5}=0,6,\ \ cosBAO=\frac{AO}{AB}=\frac{4}{5}=0,8\ \]Тогда
\[sin\alpha =2sinBAOcosBAO=2\cdot 0,6\cdot 0,8=0,96\] \[S=5^2\cdot 0,96=24\]Ответ: $24.$













