Периметр любой геометрической фигур на плоскости определяется как сумма длин всех его сторон. В этой статье, на примере задач, мы приведем формулы для нахождения периметров квадрата, прямоугольника, параллелограмма, трапеции, ромба, многоугольника и эллипса.
Периметр квадрата
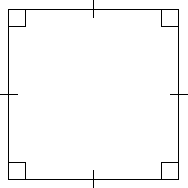
Квадратом будем назвать такую геометрическую фигуру, которая состоит из четырех равных сторон, все углы которой прямые (рис. 1).
Найти периметр квадрата, если его сторона равняется $α$.
Решение.
Так как все 4 стороны квадрата равны между собой, то, по определению периметра, получим
$P=α+α+α+α=4α$
Вывод: Для нахождения периметра квадрата надо длину его стоны умножить на $4.$
Периметр прямоугольника
Прямоугольником будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем противоположные стороны равны между собой, все углы которой прямые (рис. 2).
Найти периметр прямоугольника, если его смежные стороны равняются $α$ и $β$.
Решение.
Так как противоположные стороны равняются между собой, то
$P=α+α+β+β=2α+2β=2(α+β)$
Вывод: Для нахождения периметра прямоугольника надо сумму длин его смежных сторон умножить на $2.$
Периметр параллелограмма
Параллелограммом будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем противоположные стороны равны между собой и параллельны друг другу (рис. 3).
Найти периметр параллелограмма, если его смежные стороны равняются $α$ и $β$.
Решение.
Так как противоположные стороны равняются между собой, то
$P=α+α+β+β=2α+2β=2(α+β)$
Вывод: Для нахождения периметра параллелограмма надо сумму длин его смежных сторон умножить на $2.$
Периметр трапеции
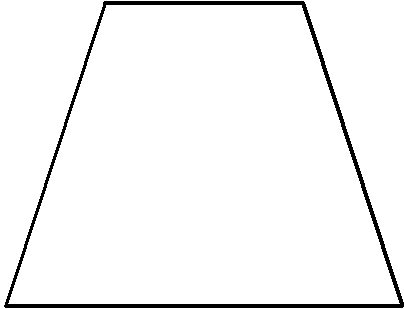
Трапецией будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем 2 противоположные стороны, которые называются основаниями, параллельны друг другу (рис. 4).
Найти периметр трапеции, если его стороны равняются $α$, $β$, $γ$ и $δ$.
Решение.
По определению периметра плоской геометрической фигуры получим, что
$P=α+β+γ+δ$
Вывод: Для нахождения периметра трапеции надо сложить все длины его сторон.
Периметр ромба
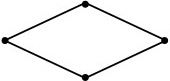
Ромбом будем назвать такой параллелограмм, у которого все стороны равны между собой (рис. 5).
Найти периметр ромба, если его сторона равняется $α$.
Решение.
Так как все 4 стороны ромба равны между собой, то, по определению периметра, получим
$P=α+α+α+α=4α$
Вывод: Для нахождения периметра ромба надо длину его стоны умножить на $4.$
Периметр многоугольника
Отметим, что все фигуры, рассмотренные выше, являются многоугольниками, а именно четырехугольниками. Поэтому можем рассмотреть более обще понятие, а именно понятие -угольника.
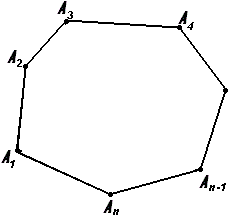
$n$-угольником будем назвать такую геометрическую фигуру, которая состоит из $n$ непересекающихся сторон и $n$ углов. (рис. 6).
Найти периметр $n$-угольника, если его стороны равняются $α_1$, $α_2$,…, $α_n$.
Решение.
По определению периметра плоской геометрической фигуры получим, что
$P=α_1+α_2+⋯+ α_n$
Вывод: Для нахождения периметра -угольника надо сложить все длины его сторон.
Здесь можно выделить периметр правильного $n$-угольника, то есть $n$-угольника, у которого все стороны равняются между собой.
Найти периметр правильного $n$-угольника, если его сторона равняется $α$.
Решение.
Так как все $n$ сторон правильного $n$-угольника равны между собой, то, по определению периметра, получим
$P=α+α+⋯+α+α$ - $n$ раз.
Следовательно
$P=nα$
Вывод: Для нахождения периметра правильного $n$-угольника надо длину его стороны умножить на $n$
Периметр эллипса
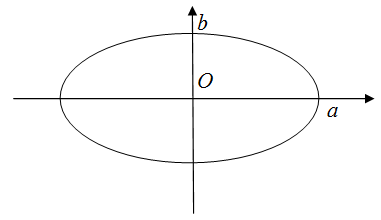
Здесь просто введем формулу, для вычисления периметра (или еще иначе длины) эллипса. Пусть нам дан эллипс, как на рисунке 7.
Тогда периметр эллипса равняется
$P=4\frac{πab+a-b}{a+b}$