Площадь параллелограмма
Площадь параллелограмма определяется как произведение длины его стороны, на высоту, проведенную к ней.
Математически это можно записать следующим образом
\[S=ah\]где $a$ сторона параллелограмма, $h$ - высота, проведенная к этой стороне.
Доказательство.
Пусть нам дан параллелограмм $ABCD$, у которого $AD=BC=a$. Проведем высоты $DF$ и $AE$ (рис. 1).
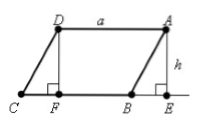
Рисунок 1.
Очевидно, что фигура $FDAE$ -- прямоугольник.
\[\angle BAE={90}^0-\angle A,\ \] \[\angle CDF=\angle D-{90}^0={180}^0-\angle A-{90}^0={90}^0-\angle A=\angle BAE\]Следовательно, так как $CD=AB,\ DF=AE=h$, по $I$ признаку равенства треугольников $\triangle BAE=\triangle CDF$. Тогда
\[S_{FDAE}=S_{ABCD}-S_{CDF}+S_{BAE}=S_{ABCD}-S_{CDF}+S_{CDF}=S_{ABCD}\]Значит по теореме о площади прямоугольника:
\[S_{ABCD}=S_{FDAE}=ah\]Теорема доказана.
Площадь параллелограмма определяется как произведение длины его смежных сторон, на синус угла между этими сторонами.
Математически это можно записать следующим образом
\[S=absin\alpha \]где $a,\ b$ стороны параллелограмма, $\alpha $ -- угол между ними.
Доказательство.
Пусть нам дан параллелограмм $ABCD$, у которого $BC=a,\ CD=b,\ \angle C=\alpha $. Проведем высоту $DF=h$ (рис. 2).
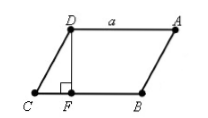
Рисунок 2.
По определению синуса, получим
\[sin\alpha =\frac{DF}{CD}=\frac{h}{b}\]Следовательно
\[h=bsin\alpha \]Значит, по теореме $1$:
\[S=ah=absin\alpha \]Теорема доказана.
Площадь треугольника
Площадь треугольника определяется как половина произведения длины его стороны, на высоту, проведенную к ней.
Математически это можно записать следующим образом
\[S=\frac{1}{2}ah\]где $a$ сторона треугольника, $h$ - высота, проведенная к этой стороне.
Доказательство.
Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).
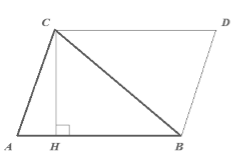
Рисунок 3.
Очевидно, что по $I$ признаку равенства треугольников $\triangle ACB=\triangle CDB$. Тогда
\[S_{ABC}=\frac{1}{2}S_{ABCD}\]Значит по теореме $1$:
\[S_{ABC}=\frac{1}{2}ah\]Теорема доказана.
Площадь треугольника определяется как половина произведения длины его смежных сторон, на синус угла между этими сторонами.
Математически это можно записать следующим образом
\[S=\frac{1}{2}absin\alpha \]где $a,\ b$ стороны треугольника, $\alpha $ -- угол между ними.
Доказательство.
Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).
Очевидно, что по $I$ признаку равенства треугольников $\triangle ACB=\triangle CDB$. Тогда
\[S_{ABC}=\frac{1}{2}S_{ABCD}\]Значит по теореме $1$:
\[S_{ABC}=\frac{1}{2}absin\alpha \]Теорема доказана.
Площадь трапеции
Площадь трапеции определяется как половина произведения суммы длин его оснований, на его высоту.
Математически это можно записать следующим образом
\[S=\frac{1}{2}(a+b)h\]Доказательство.
Пусть нам дана трапеция $ABCK$, где $AK=a,\ BC=b$. Проведем в ней высоты $BM=h$ и $KP=h$, а также диагональ $BK$ (рис. 4).
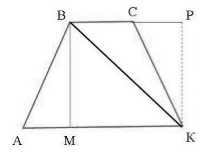
Рисунок 4.
По теореме $3$, получим
\[S_{ABK}=\frac{1}{2}AK\cdot BM=\frac{1}{2}ah,\ S_{BCK}=\frac{1}{2}BC\cdot KP=\frac{1}{2}bh\]Тогда
\[S_{ABCK}=\frac{1}{2}ah+\frac{1}{2}bh=\frac{1}{2}(a+b)h\]Теорема доказана.
Пример задачи
Найти площадь равностороннего треугольника, если длина его стороны равняется $a.$
Решение.
Так как треугольник равносторонний, то все его углы равняются ${60}^0$.
Тогда, по теореме $4$, имеем
\[S=\frac{1}{2}a\cdot a\cdot sin{60}^0=\frac{a^2\sqrt{3}}{4}\]Ответ: $\frac{a^2\sqrt{3}}{4}$.
Заметим, что результат этой задачи можно применять при нахождении площади любого равностороннего треугольника с данной стороной.













