Формула Эйлера названа именем известного математика Л. Эйлера, который ввел данную формулу. Формула Эйлера позволяет связать комплексную экспоненту (показательную функцию) с тригонометрическими функциями.
Формула Эйлера утверждает, что для любого вещественного (действительного) и комплексного числа $x$ выполняется следующее равенство:
где $e$ -- экспонента, $i$ -- мнимая единица.
Экспонента определяется следующей формулой:
Для некоторого комплексного числа $z=x+yi$ выполняется:
В случае, когда $z$ является вещественным числом $(Imz=0)$, получаем
Если $z$ является чисто мнимым числом $(Rez=0)$, получаем:
Далее используя формулу Эйлера, получаем следующее:
Рассмотрим некоторое комплексное число $z$, записанное в тригонометрической форме $z=r(\cos \varphi +i\cdot \sin \varphi )$, где $r=|z|=\sqrt{x^{2} +y^{2} } $ является модулем этого комплексного числа. С помощью формулы Эйлера, получаем
С помощью формулы Эйлера появляется возможность определить функции $\sin $ и $\cos $ следующими формулами:
Введем понятие тригонометрических функций от комплексной переменной. Для $x=iy$ получаем следующие формулы:
Известное тождество Эйлера, которое связывает пять фундаментальных математических констант:
является частным случаем формулы Эйлера при значении переменной $x=\pi $.
Благодаря формуле Эйлера появились тригонометрическая и показательная формы представления комплексного числа.
Представление некоторого комплексного числа $z$ в виде $z=r\cdot (\cos \varphi +i\sin \varphi )$ называется тригонометрической формой записи, где число $r$ является модулем комплексного числа $z$, который определяется по формуле $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, $\varphi $ является аргументом комплексного числа $z$, который определяется по формуле $\varphi =arctg\frac{b}{a} $.
Рассмотрим комплексное число, представленное в тригонометрической форме
С помощью формулы Эйлера, получим:
Подставим полученное значение в тригонометрическую запись некоторого комплексного числа и получим:
Представление некоторого комплексного числа $z$ в виде $z=r\cdot e^{i\varphi } $ называется показательной формой записи, где число $r$ является модулем комплексного числа $z$, который определяется по формуле $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, $\varphi $ является аргументом комплексного числа $z$, который определяется по формуле $\varphi =arctg\frac{b}{a} $.
Значительным следствием из формулы Эйлера считаются формулы возведения некоторого комплексного числа в степень с произвольным показателем:
Геометрический смысл последней формулы таков: при возведении некоторого числа $z$ в заданную степень $n$ его модуль (расстояние до центра) возводится в заданную степень $n$, а аргумент (угол поворота относительно оси $OX$) увеличивается соответственно в $n$ раз (рис. 1).
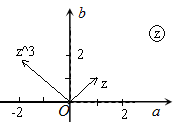
Рис. 1.
Формула возведения в степень заданного комплексного числа верна не только для целых $n$, но и для действительных чисел. В частности, комплексная форма представления числа позволяет найти корни любой степени из произвольного комплексного числа.
Представить заданные комплексные числа в показательной форме:
1) $z=2+0\cdot i$; 2) $z=\frac{3}{2} +\frac{3}{2} \cdot i$.
Решение:
Показательная форма представления некоторого комплексного числа имеет следующий вид $z=r\cdot e^{i\varphi } $.
1) По условию $a=2,b=0$.
Вычислим модуль исходного комплексного числа:
Вычислим аргумент исходного комплексного числа, используя формулу (*):
Подставим полученные значения и получим:
Следовательно, $z=2\cdot e^{i\cdot 0} $ - искомое представление комплексного числа.
2) По условию $a=\frac{3}{2} ,b=\frac{3}{2} $.
Вычислим модуль исходного комплексного числа:
Вычислим аргумент исходного комплексного числа, используя формулу (*):
Подставим полученные значения и получим:
Следовательно, $z=\frac{3\sqrt{2} }{2} \cdot e^{i\cdot \frac{\pi }{4} } $ - искомое представление комплексного числа.
Представить заданные комплексные числа в показательной форме:
1) $z=\sqrt{3} \cdot (\cos \frac{\pi }{6} +i\sin \frac{\pi }{6} )$; 2) $z=5\cdot (\cos 2\pi +i\sin 2\pi )$.
Решение:
Показательная форма представления некоторого комплексного числа имеет следующий вид $z=r\cdot e^{i\varphi } $.
1) Определим значения модуля и аргумента: $r=\sqrt{3} ,\, \, \varphi =\frac{\pi }{6} $.
Представление числа в показательной форме имеет следующий вид: $z=\sqrt{3} \cdot e^{\frac{\pi }{6} \cdot i} $.
2) Определим значения модуля и аргумента: $r=5,\, \, \varphi =2\pi $.
Представление числа в показательной форме имеет следующий вид: $z=5\cdot e^{2\pi \cdot i} $.
Представить заданные комплексные числа в алгебраической форме:
1) $z=3\cdot e^{\frac{\pi }{3} \cdot i} $; 2) $z=6\cdot e^{\pi \cdot i} $.
Решение:
Алгебраическая форма представления некоторого комплексного числа имеет следующий вид $z=a+bi$.
1) Запись числа в тригонометрической форме имеет следующий вид: $z=3\cdot (\cos \frac{\pi }{3} +i\sin \frac{\pi }{3} )$.
По таблице косинусов и синусов $\cos \frac{\pi }{3} =\frac{1}{2} ;\sin \frac{\pi }{3} =\frac{\sqrt{3} }{2} $.
Подставим значения и выполним преобразования и вычисления:
Следовательно, $z=\frac{3}{2} +\frac{3\sqrt{3} }{2} \cdot i$ - искомая запись комплексного числа.
2) Запись числа в тригонометрической форме представления имеет следующий вид: $z=6\cdot (\cos \pi +i\sin \pi )$.
По таблице косинусов и синусов $\cos \pi =-1;\sin \pi =0$.
Подставим значения и выполним преобразования и вычисления:
Следовательно, $z=-1+0\cdot i$ - искомое представление комплексного числа.












