Введем сначала определение показательной функции.
Функция $f\left(x\right)=a^x$, где $a>0,\ a\ne 1$, называется показательной функцией.
Далее будем рассматривать два отдельных случая: когда $01$.
Показательная функция $f\left(x\right)=a^x$, где $a >1$.
Введем свойства показательной функции, при $a >1$.
-
Область определения -- все действительные числа.
-
$f\left(-x\right)=a^{-x}=\frac{1}{a^x}$ -- функция ни четна, ни нечетна.
-
$f(x)$ - непрерывна на всей области определения.
-
Область значения -- интервал $(0,+\infty )$.
-
$f'(x)=\left(a^x\right)'=a^xlna$
\[a^xlna=0\] \[корней\ нет.\] \[f'\left(x\right) >0\]Функция возрастает на всей области определения.
-
$f(x)\ge 0$ на всей области определения.
-
Пересечение с осями координат. Функция не пересекает ось $Ox$, но пересекает ось $Oy$ в точке $(0,1)$.
-
$f''\left(x\right)={\left(a^xlna\right)}'=a^x{ln}^2a$
\[a^x{ln}^2a=0\] \[корней\ нет.\] \[f''\left(x\right) >0\]Функция выпукла на всей области определения.
-
Поведение на концах области определения:
\[{\mathop{lim}_{x\to -\infty } a^x\ }=0\] \[{\mathop{lim}_{x\to +\infty } a^x\ }=+\infty \] -
График (рис. 1).
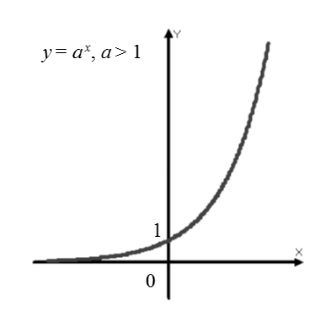График функции $f\left(x\right)=a^x,\ при\ a >1$.">
Рисунок 1. График функции $f\left(x\right)=a^x,\ при\ a >1$.
Показательная функция $f\left(x\right)=a^x$, где $0
Введем свойства показательной функции, при $0
-
Область определения -- все действительные числа.
-
$f\left(-x\right)=a^{-x}=\frac{1}{a^x}$ -- функция ни четна, ни нечетна.
-
$f(x)$ - непрерывна на всей области определения.
-
Область значения -- интервал $(0,+\infty )$.
-
$f'(x)=\left(a^x\right)'=a^xlna$
\[a^xlna=0\] \[корней\ нет.\] \[f'\left(x\right)Функция убывает на всей области определения. -
$f(x)\ge 0$ на всей области определения.
-
Пересечение с осями координат. Функция не пересекает ось $Ox$, но пересекает ось $Oy$ в точке ($0,1)$.
-
$f''\left(x\right)={\left(a^x{ln}^2a\right)}'=a^x{ln}^3a$
\[a^x{ln}^3a=0\] \[корней\ нет.\] \[f''\left(x\right)>0\]Функция выпукла на всей области определения.
-
Поведение на концах области определения:
\[{\mathop{lim}_{x\to -\infty } a^x\ }=+\infty \] \[{\mathop{lim}_{x\to +\infty } a^x\ }=0\] -
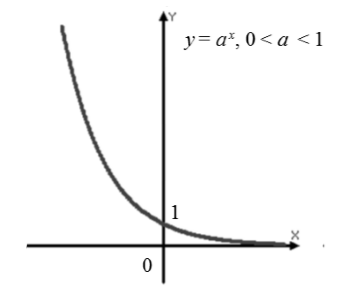
График (рис. 2).
Пример задачи на построение показательной функции
Исследовать и построить график функции $y=2^x+3$.
Решение.
Проведем исследование по примеру схемы выше:
-
Область определения -- все действительные числа.
-
$f\left(-x\right)=2^{-x}+3$ -- функция ни четна, ни нечетна.
-
$f(x)$ - непрерывна на всей области определения.
-
Область значения -- интервал $(3,+\infty )$.
-
$f'\left(x\right)={\left(2^x+3\right)}'=2^xln2>0$
Функция возрастает на всей области определения.
-
$f(x)\ge 0$ на всей области определения.
-
Пересечение с осями координат. Функция не пересекает ось $Ox$, но пересекает ось $Oy$ в точке ($0,4)$
-
$f''\left(x\right)={\left(2^xln2\right)}'=2^x{ln}^22>0$
Функция выпукла на всей области определения.
-
Поведение на концах области определения:
\[{\mathop{lim}_{x\to -\infty } a^x\ }=0\] \[{\mathop{lim}_{x\to +\infty } a^x\ }=+\infty \] -
График (рис. 3).
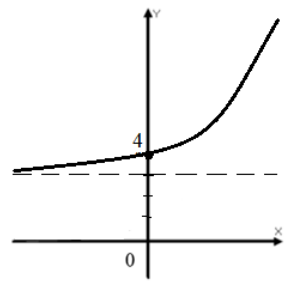
Рисунок 3. График функции $f\left(x\right)=2^x+3$
