Показательное распределение

Источник статьи

Автор24 — учеба по твоим правилам

Отметим здесь основные понятия и формулы, связанные с показательным распределением непрерывной случайной величины $X$ не вдаваясь в подробности их вывода.

Определение 1

Показательным или экспоненциальным распределения непрерывной случайной величины $X$ называется распределение, плотность которого имеет вид:

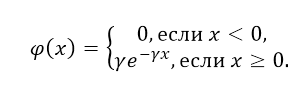
Рисунок 1.

где $\gamma $ - положительная константа.

График плотности показательного распределения имеет вид (рис. 1):

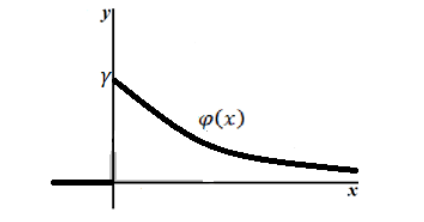
Рисунок 2. График плотности показательного распределения.

Функция показательного распределения

Как нетрудно проверить, функция показательного распределения имеет вид:

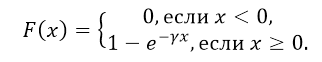
Рисунок 3.

где $\gamma $ - положительная константа.

График функции показательного распределения имеет вид:

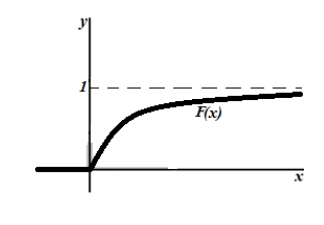
Рисунок 4. График функции показательного распределения.

Вероятность попадания случайной величины при показательном распределении

Вероятность попадания непрерывной случайной величины в интервал $(\alpha ,\beta )$ при показательном распределении вычисляется по следующей формуле:

Математическое ожидание: $M\left(X\right)=\frac{1}{\gamma }.$

Дисперсия: $D\left(X\right)=\frac{1}{{\gamma }^2}.$

Среднее квадратическое отклонение: $\sigma \left(X\right)=\frac{1}{\gamma }$.

Пример задачи на показательное распределение

Пример 1

Случайная величина $X$ подчиняется экспоненциальному закону распределения. На участке области определения $\left[0,\infty )\right.$ случайная величина $X$ имеет плотность вида $\varphi \left(x\right)=\alpha e^{-3x}$.

Найти плотность распределения и построить её график.
Найти функцию распределения и построить её график.
Найти вероятность того, что случайная величина попадет в интервал $(0,2;;0,4)$.
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение данного распределения.

Решение:

Так как случайная величина подчиняется показательному закону распределения, то $\alpha =3.$ Таким образом, плотность данного распределения будет иметь вид:

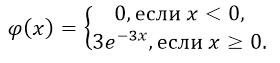
Рисунок 5.

Построим её график. Максимальное значения функция плотности распределения достигнет в точке $\left(0,\gamma \right)=(0,3)$

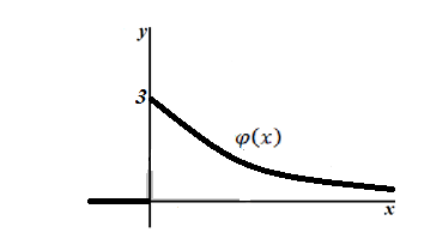
Рисунок 6.

Так как $\gamma =3$, то по формуле функции показательного распределения, функция распределения в нашем случае будет иметь вид:

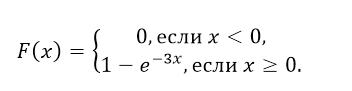
Рисунок 7.

При $x=1,\ F\left(1\right)=1-e^{-3}=1-0,05=0,95$, получаем график

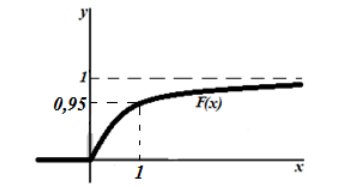
Рисунок 8.

Для нахождения искомой вероятности будем пользоваться следующей формулой:

\[P\left(\alpha Получим: \[P\left(0,2Для нахождения значений функции $y=e^{-x}$ существуют специальные таблицы, из них легко находим, что $e^{-0,6}=0,549,\ e^{-1,2}=0,302$. Значит: \[P\left(0,2

Для нахождения характеристик воспользуемся выше данными формулами:

\[M\left(X\right)=\sigma \left(X\right)=\frac{1}{\gamma }=\frac{1}{3}.\] \[D\left(X\right)=\frac{1}{{\gamma }^2}=\frac{1}{9}.\]

Дата последнего обновления статьи: 20.02.2024