Напомним, что плотность показательного распределения имеет вид:
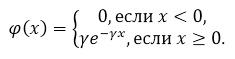
Рисунок 1.
Математическое ожидание
Математическое ожидание вычисляется по формуле:
Рассмотрим сначала неопределенный интеграл $\int{xe^{-\gamma x}dx}$
Значит:
Дисперсия
Дисперсия находится по следующей формуле:
Как было рассмотрено выше:
Значит:
Рассмотрим неопределенный интеграл $\int{x^2e^{-\gamma x}dx}$
Тогда:
Получаем:
Среднее квадратическое ожидание
Среднее квадратическое ожидание найдем по формуле
Получим:
!!! Отметим, что в случае показательного распределения значения математического ожидания и среднего квадратического отклонения равны.
Примеры решения задач на нахождение числовых характеристик показательного распределения
Плотность распределения непрерывной случайной величины имеет следующий вид:
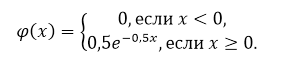
Рисунок 2.
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
Решение.
Так как плотность имеет такой вид, то в нашем случае непрерывная случайная величина подчиняется показательному закону с коэффициентом $\gamma =0,5.$ Значит значение математического ожидания $M(X)$, дисперсии $D(X)$ и среднего квадратического отклонения $\sigma (X)$ найдем по формулам, выведенным выше:
\[M\left(X\right)=\frac{1}{0,5}=\frac{10}{5}=2\] \[D\left(X\right)=\frac{1}{{0,5}^2}=\frac{1}{0,25}=\frac{100}{25}=4\] \[\sigma \left(X\right)=M\left(X\right)=2\]$96\%$ моторов автомобилей, произведенных за год, ломаются в течении первых $8000 часов$ работы. Определить среднее время безотказной работы таких моторов, дисперсию и среднее квадратическое отклонение (Распределение считать экспоненциальным).
Решение:
По определению потенциального распределения, плотность распределения имеет вид:
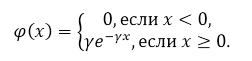
Рисунок 3.
Для начала необходимо найти константу $\gamma $. Из условия задачи, получаем:
\[P\left(X\ge 8000\right)=0,96.\]Найдем $P\left(X\ge 8000\right)$:
\[P\left(X\ge 8000\right)=1-P\left(XКак нам уже известно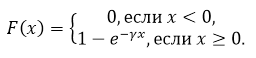
Рисунок 4.
Значит
\[F\left(8000\right)=1-e^{-8000\gamma }\]Получаем уравнение:
\[1-1+e^{-8000\gamma }=0,96,\] \[e^{-8000\gamma }=0,96,\] \[-8000\gamma =ln0,96,\] \[\gamma =-\frac{ln0,96}{8000}=0,000005\]Получаем, что плотность распределения имеет вид:
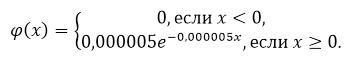
Рисунок 5.
Найдем теперь все характеристике по выше выведенным формулам.
(Отметим, что математическое ожидание -- это и есть время безотказной работы).
\[M\left(X\right)=\frac{1}{0,000005}=\frac{1000000}{5}=200000\] \[D\left(X\right)=\frac{1}{{0,000005}^2}=\frac{1}{0,000000000025}=\frac{1000000000000}{25}=4\cdot {10}^{10}\] \[\sigma \left(X\right)=M\left(X\right)=200000\]













