Для удобства рассмотрения степенной функции будем рассматривать 4 отдельных случая: степенная функция с натуральным показателем, степенная функция с целым показателем, степенная функция с рациональным показателем и степенная функция с иррациональным показателем.
Степенная функция с натуральным показателем
Для начала введем понятие степени с натуральным показателем.
Степенью действительного числа $a$ с натуральным показателем $n$ называется число, равное произведению $n$ множителей, каждый из которых равняется числу $a$.
Рисунок 1.
$a$ - основание степени.
$n$ - показатель степени.
Рассмотрим теперь степенную функцию с натуральным показателем, её свойства и график.
$f\left(x\right)=x^n$ ($n\in N)$ называется степенной функцией с натуральным показателем.
Для дальнейшего удобства рассмотрим отдельно степенную функцию с четным показателем $f\left(x\right)=x^{2n}$ и степенную функцию с нечетным показателем $f\left(x\right)=x^{2n-1}$ ($n\in N)$.
Свойства степенной функции с натуральным четным показателем
-
Область определения -- все действительные числа.
-
$f\left(-x\right)={(-x)}^{2n}=x^{2n}=f(x)$ -- функция четна.
-
$f(x)$ - непрерывна на всей области определения.
-
Область значения -- $[0,+\infty )$.
-
$f'(x)=\left(x^{2n}\right)'=2n\cdot x^{2n-1}$
\[2n\cdot x^{2n-1}=0\] \[x=0\]Функция убывает, при $x\in (-\infty ,0)$ и возрастает, при $x\in (0,+\infty )$.
-
$f(x)\ge 0$ на всей области определения
-
$f{''}\left(x\right)={\left(2n\cdot x^{2n-1}\right)}'=2n(2n-1)\cdot x^{2(n-1)}\ge 0$
Функция выпукла на всей области определения.
-
Поведение на концах области определения:
\[{\mathop{lim}_{x\to -\infty } x^{2n}\ }=+\infty \] \[{\mathop{lim}_{x\to +\infty } x^{2n}\ }=+\infty \] -
График (рис. 2).
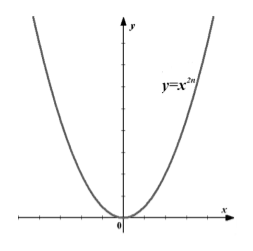График функции $f\left(x\right)=x^{2n}$">
Рисунок 2. График функции $f\left(x\right)=x^{2n}$
Свойства степенной функции с натуральным нечетным показателем
-
Область определения -- все действительные числа.
-
$f\left(-x\right)={(-x)}^{2n-1}={-x}^{2n}=-f(x)$ -- функция нечетна.
-
$f(x)$ - непрерывна на всей области определения.
-
Область значения -- все действительные числа.
-
$f'\left(x\right)=\left(x^{2n-1}\right)'=(2n-1)\cdot x^{2(n-1)}\ge 0$
Функция возрастает на всей области определения.
-
$f\left(x\right)0$, при $x\in (0,+\infty )$.
-
$f{''\left(x\right)}={\left(\left(2n-1\right)\cdot x^{2\left(n-1\right)}\right)}'=2\left(2n-1\right)(n-1)\cdot x^{2n-3}$
\[2\left(2n-1\right)\left(n-1\right)\cdot x^{2n-3}=0\] \[x=0\]Функция вогнута, при $x\in (-\infty ,0)$ и выпукла, при $x\in (0,+\infty )$.
-
График (рис. 3).
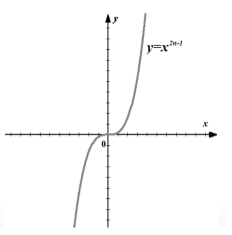
Рисунок 3. График функции $f\left(x\right)=x^{2n-1}$
Степенная функция с целым показателем
Для начала введем понятие степени с целым показателем.
Степень действительного числа $a$ c целым показателем $n$ определяется формулой:
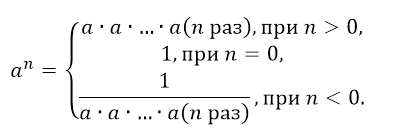
Рисунок 4.
Рассмотрим теперь степенную функцию с целым показателем, её свойства и график.
$f\left(x\right)=x^n$ ($n\in Z)$ называется степенной функцией с целым показателем.
Если степень больше нуля, то мы приходим к случаю степенной функции с натуральным показателем. Его мы уже рассмотрели выше. При $n=0$ мы получим линейную функцию $y=1$. Её рассмотрение оставим читателю. Осталось рассмотреть свойства степенной функции с отрицательным целым показателем
Свойства степенной функции с отрицательным целым показателем
-
Область определения -- $\left(-\infty ,0\right)(0,+\infty )$.
-
Если показатель четный, то функция четна, если нечетный, то функция нечетна.
-
$f(x)$ - непрерывна на всей области определения.
-
Область значения:
Если показатель четный, то $(0,+\infty )$, если нечетный, то $\left(-\infty ,0\right)(0,+\infty )$.
-
При нечетном показателе функция убывает, при $x\in \left(-\infty ,0\right)(0,+\infty )$. При четном показателе функция убывает при $x\in (0,+\infty )$. и возрастает, при $x\in \left(-\infty ,0\right)$.
-
$f(x)\ge 0$ на всей области определения
-
График (рис. 4).
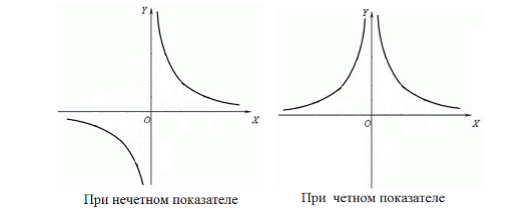
Степенная функция с рациональным и иррациональным показателем
Степень действительного числа $a$ c рациональным показателем $n$ определяется формулой:
\[a^r=\sqrt[n]{a^m}\]$f\left(x\right)=x^r$ ($r\in Q)$ называется степенной функцией с рациональным показателем.
Степень положительного числа $a$ c иррациональным показателем $\alpha $ называется выражение вида $a^{\alpha }$, значение которого равно пределу последовательности $a^{{\alpha }_0},\ a^{{\alpha }_1},\ a^{{\alpha }_2},\dots $, где ${\alpha }_0,\ {\alpha }_1,{\alpha }_2$ последовательные десятичные приближения иррационального числа $\alpha $.
$f\left(x\right)=x^r$ ($r\in J)$ называется степенной функцией с иррациональным показателем.
Приведем графики степенных функций с рациональным и иррациональным показателем (рис. 5). Рассмотреть, аналогично, свойства этих функции оставим читателю.
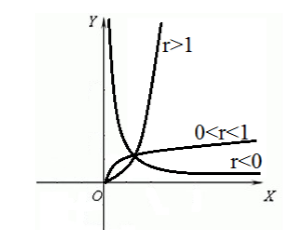
Рисунок 6. График функции $f\left(x\right)=x^r$
