Определение
Функция, обратная к показательной функции f(x) = ax при a ≠ 1 называется логарифмической функцией по основанию а и обозначается logax, т.е.f -1(x) = logax.
Область определения логарифмической функции $D(log_ax) = (0, \infty )\ $
Множество значений логарифмической функции $R(log_ax) = (- \infty ,\infty )$.
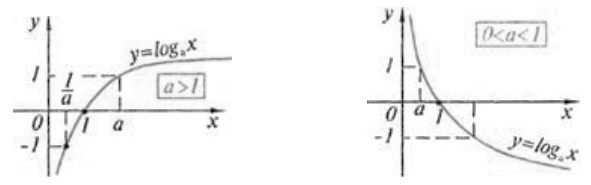
Рисунок 1. График логарифмической функции
Логарифмическое дифференцирование является методом дифференцирования функции $y = f(x)$.
Алгоритм дифференцирования
- Взять натуральные логарифмы от выражения y = f(x).
- Продифференцировать правую и левую часть по х. \[\left(\ln y\right){{'} } =\frac{y'}{y} \]
- Решить получающееся уравнение относительно y '.
Замечание
Если $f(x) \[\left|y\right|=\left|f(x)\right|\] \[\frac{d}{dx} (\ln \left|x\right|)=\frac{1}{x} \]
Пример 1
Найти производную функции
\[y=\cos x^{arctgx} \]Решение.
- Возьмем натуральные логарифмы \[\ln y=\ln (\cos x)^{arctgx} \] \[\ln y=arctgx\cdot \ln (\cos x)\]
- Продифференцируем выражение \[\frac{1}{y} y'=\frac{\ln \cos x}{1+x^{2} } +arctgx\cdot \frac{1}{\cos x} (-\sin x)=\frac{\ln \cos x}{1+x^{2} } -arctgx\cdot tgx\]
- Выразим y' \[y'=y\left(\frac{\ln \cos x}{1+x^{2} } +arctgx\cdot \frac{1}{\cos x} (-\sin x)=\frac{\ln \cos x}{1+x^{2} } -arctgx\cdot tgx\right)\]
- Заменим y \[y'=(\cos x)^{arctgx} \left[\frac{\ln \cos x}{1+x^{2} } -arctgx\cdot tgx\right]\]
Пример 2
Найти производную функции
\[y=(x^{3} -1)^{tg2x} \]Решение.
- Возьмем натуральные логарифмы \[\ln y=\ln (x^{3} -1)^{tg2x} \] \[\ln y=tg2x\cdot \ln (x^{3} -1)\]
- Продифференцируем выражение \[\left(\ln y\right){{'} } =\left(tg2x\cdot \ln (x^{3} -1)\right){{'} } \] \[\frac{y{{'} } }{y} =\left(tg2x\cdot \ln (x^{3} -1)\right){{'} } \] \[\frac{y{{'} } }{y} =tg2x'\cdot \ln (x^{3} -1)+tg2x\cdot \ln (x^{3} -1)'\] \[\frac{y{{'} } }{y} =\frac{2}{\cos ^{2} 2x} \cdot \ln (x^{3} -1)+tg2x\cdot \frac{3x^{2} }{x^{3} -1} \]
- Выразим y' \[y{{'} } =y\left(\frac{2\ln (x^{3} -1)}{\cos ^{2} 2x} +\frac{3x^{2} tg2x}{x^{3} -1} \right)\]
- Заменим y \[y{{'} } =(x^{3} -1)^{tg2x} \left(\frac{2\ln (x^{3} -1)}{\cos ^{2} 2x} +\frac{3x^{2} tg2x}{x^{3} -1} \right)\]
Пример 3
Найти производную функции
\[y=\left(\cos (x-1)\right)^{\ln x} \]Решение.
- Возьмем натуральные логарифмы \[\ln y=\ln \left(\cos (x-1)\right)^{\ln x} \] \[\ln y=\ln x\ln \left(\cos (x-1)\right)\]
- Продифференцируем выражение \[\left(\ln y\right){{'} } =\left(\ln x\cdot \ln \left(\cos (x-1)\right)\right){{'} } \] \[\frac{y{{'} } }{y} =\ln x'\cdot \ln \left(\cos (x-1)\right)+\ln x\cdot \ln \left(\cos (x-1)\right){{'} } \] \[\frac{y{{'} } }{y} =\frac{1}{x} \cdot \ln \left(\cos (x-1)\right)+\ln x\cdot \frac{1}{\cos (x-1)} \left(\cos (x-1)\right){{'} } \] \[\frac{y{{'} } }{y} =\frac{\ln \left(\cos (x-1)\right)}{x} -\frac{\sin (x-1)\ln x}{\cos (x-1)} \]
- Выразим y' \[y{{'} } =y\left(\frac{\ln \left(\cos (x-1)\right)}{x} -\frac{\sin (x-1)\ln x}{\cos (x-1)} \right)\]
- Заменим y \[y{{'} } =\left(\cos (x-1)\right)^{\ln x} \left(\frac{\ln \left(\cos (x-1)\right)}{x} -\frac{\sin (x-1)\ln x}{\cos (x-1)} \right)\]
Дата последнего обновления статьи: 15.12.2024
