Экстремумы функции
Точки $x_0$ называются точками экстремума функции, если они являются точками максимума и минимума для функции $f(x)$.
Точка $x_0$ называется точкой максимума функции $f(x)$, если существует такая окрестность данной точки, что для всех $x$ из этой окрестность выполняется неравенство $f(x)\le f(x_0)$.
Точка $x_0$ называется точкой максимума функции $f(x)$, если существует такая окрестность данной точки, что для всех $x$ из этой окрестность выполняется неравенство $f(x)\ge f(x_0)$.
Понятие экстремума функции тесно связано с понятием критической точки функции. Введем её определение.
$x_0$ называется критической точкой функции $f(x)$, если:
1) $x_0$ - внутренняя точка области определения;
2) $f'\left(x_0\right)=0$ или не существует.
Для понятия экстремума можно сформулировать теоремы о достаточных и необходимых условиях его существования.
Необходимое условие экстремума
Если функция $y=f(x)$ имеет экстремум в точке $x_0$, то либо $f'\left(x_0\right)=0$, либо производная в точке $x_0$ не существует.
Достаточное условие экстремума
Пусть точка $x_0$ является критической для функции $y=f(x)$ и лежит в интервале $(a,b)$. Пусть на каждом интервале $\left(a,x_0\right)\ и\ (x_0,b)$ производная $f'(x)$ существует и сохраняет постоянный знак. Тогда:
1) Если на интервале $(a,x_0)$ производная $f'\left(x\right)>0$, а на интервале $(x_0,b)$ производная $f'\left(x\right)
2) Если на интервале $(a,x_0)$ производная $f'\left(x\right)0$, то точка $x_0$ - точка минимума для данной функции.
3) Если и на интервале $(a,x_0)$, и на интервале $(x_0,b)$ производная $f'\left(x\right) >0$ или производная $f'\left(x\right)
Данная теорема проиллюстрирована на рисунке 1.
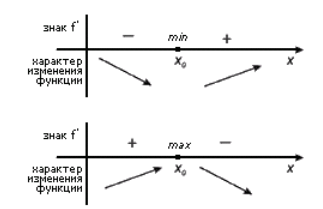
Рисунок 1. Достаточное условие существования экстремумов
Примеры экстремумов (Рис. 2).
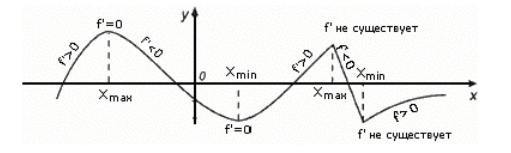
Рисунок 2. Примеры точек экстремумов
Правило исследования функции на экстремум
1) Найти область определения функции $f(x)$;
2) Найти производную $f'(x)$;
3) Найти точки, в которых выполняется равенство $f'\left(x\right)=0$;
4) Найти точки, в которых $f'(x)$ не существует;
5) Отметить на координатной прямой все найденные точки и область определения данной функции;
6) Определить знак производной $f'(x)$ на каждом получившемся промежутке;
7) Сделать выводы о наличии максимумов и минимумов на каждом промежутке, используя теорему 2.
Возрастание и убывание функции
Введем, для начала, определения возрастающей и убывающей функций.
Функция $y=f(x)$, определенная на промежутке $X$, называется возрастающей, если для любых точек $x_1,x_2\in X$ при $x_1
Функция $y=f(x)$, определенная на промежутке $X$, называется убывающей, если для любых точек $x_1,x_2\in X$ при $x_1f(x_2)$.
Исследование функции на возрастание и убывание
Исследовать функции на возрастание и убывание можно с помощью производной.
Для того чтобы исследовать функцию на промежутки возрастания и убывания, необходимо сделать следующее:
1) Найти область определения функции $f(x)$;
2) Найти производную $f'(x)$;
3) Найти точки, в которых выполняется равенство $f'\left(x\right)=0$;
4) Найти точки, в которых $f'(x)$ не существует;
5) Отметить на координатной прямой все найденные точки и область определения данной функции;
6) Определить знак производной $f'(x)$ на каждом получившемся промежутке;
7) Сделать вывод: на промежутках, где $f'\left(x\right)0$ функция возрастает.
Примеры задач на исследования функций на возрастание, убывание и наличие точек экстремумов
Исследовать функцию на возрастание и убывание, и наличие точек максимумов и минимумов: $f(x)={2x}^3-15x^2+36x+1$
Так как первые 6 пунктов совпадают, проведем для начала их.
1) Область определения - все действительные числа;
2) $f'\left(x\right)=6x^2-30x+36$;
3) $f'\left(x\right)=0$;
\[6x^2-30x+36=0\] \[x^2-5x+6=0\] \[x=3,\ x=2\]4) $f'(x)$ существует во всех точках области определения;
5) Координатная прямая:

Рисунок 3.
6) Определить знак производной $f'(x)$ на каждом промежутке:
\[f'\left(x\right) >0,\ при\ \left(-\infty ,2\right)\ (3,+\infty )\] \[f'\left(x\right)7) Изобразим все на одном рисунке: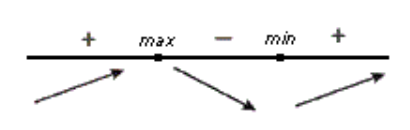
Рисунок 4.
Получаем:
Функция возрастает, при $\left(-\infty ,2\right)\ (3,+\infty )$, функция убывает, при $\left(2,3\right)$.
Точка $x=2$ - точка максимума, точка $x=3$ - точка минимума.


















