Рассмотрим и сравним график функции и ее производной (рис.1)
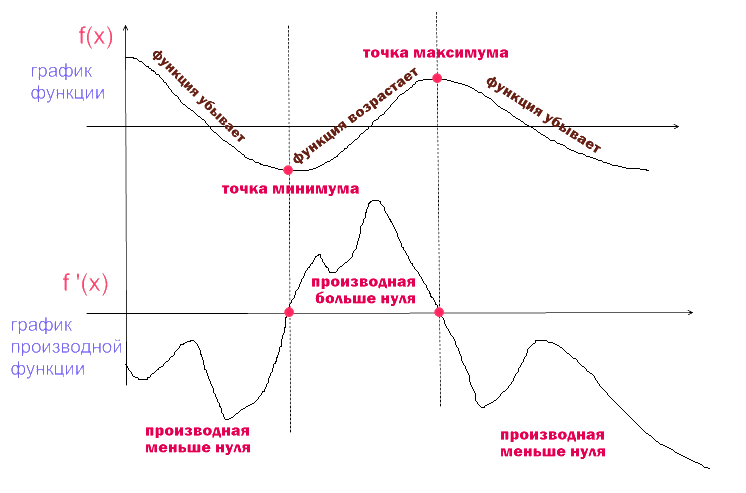
Рисунок 1. График производной
Свойства графика производной
- На интервалах возрастания производная положительна. Если производная в определённой точке из некоторого интервала имеет положительное значение, то график функции на этом интервале возрастает.
- На интервалах убывания производная отрицательна (со знаком минус). Если производная в определённой точке из некоторого интервала имеет отрицательное значение, то график функции на этом интервале убывает.
- Производная в точке х равна угловому коэффициенту касательной, проведённой к графику функции в этой же точке.
- В точках максимума-минимума функции производная равна нулю. Касательная к графику функции в этой точке параллельна оси ОХ.
По графику (рис.2) производной определить, в какой точке на отрезке [-3; 5] функция максимальна.
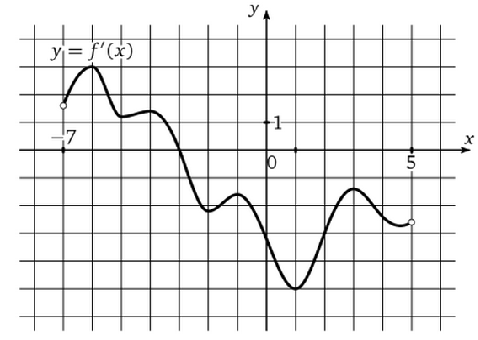
Рисунок 2. График производной
Решение: На данном отрезке производная -- отрицательна, а значит, функция убывает слева направо, и наибольшее значение находится с левой стороны в точке -3.
По графику (рис.3) производной определить количество точек максимума на отрезке [-11; 3].
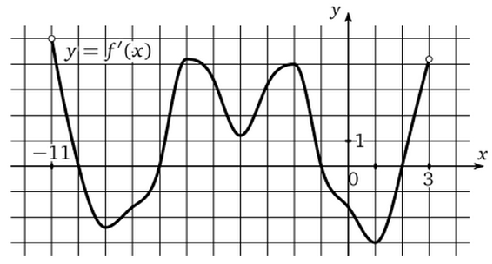
Рисунок 3. График производной
Решение: Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. На данном промежутке функция два раза меняет знак с плюса на минус -- в точке -10 и в точке -1. Значит количество точек максимума -- две.
По графику (рис.3) производной определить количество точек минимума отрезке [-11; -1].
Решение: Точки минимума соответствуют точкам смены знака производной с отрицательного на положительный. На данном отрезке такой точкой является только -7. Значит, количество точек минимума на заданном отрезке -- одна.
По графику (рис.3) производной определить количество точек экстремума.
Решение: Экстремумом являются точки как минимума, так и максимума. Найдем количество точек, в которых производная меняет знак:
- Точка -10 (максимум)
- Точка -7 (минимум)
- Точка -1 (максимум)
- Точка 2 (минимум)
Функция содержит 4 экстремума.
По графику (рис.4) производной определить количество целых точек на промежутке убывания.
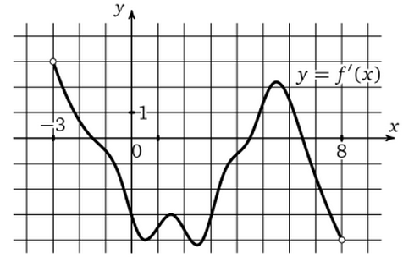
Рисунок 4. График производной
Решение: Интервалам убывания соответствуют (-3,-1.5) и (4.5,6.5). Количество целых точек по прямой х: 2(на первом промежутке) и 2 (на втором промежутке).
Ответ: 4












