Определение функции
$y=f(x)$ называется функцией, если для любого значения $x$ из множества $D\ (D\in {\mathbb R}{\rm )}$ каким-либо образом определен единственный элемент $y$ из множества $E\ (E\in {\mathbb R}{\rm )}$.
В этом определении множество $D$ называется областью определения функции, а множество $E$ - областью значения функции.
$x$ -- независимая переменная.
$y$ - зависимая переменная (значение функции).
Способы задания функции
Существуют три основных способа задания функции: аналитический, табличный и графический. Рассмотрим подробнее каждый из этих способов.
Аналитический способ
Здесь для начала введем понятие аналитического выражения.
Аналитическое выражение -- совокупность известных математических операций, которые производятся в определенно последовательности над числами и переменными величинами.
В основу аналитического способа здания функции лежит задание функции с помощью аналитического выражения.
Примеры: $y=x^2+5x+3$, $y=\frac{x+1}{x+2}$, $y=cos2x$.
Преимущества:
- Формулы определяют значение функции для любого значения независимой переменной;
- Возможность при изучении функции пользоваться аппаратом математического анализа.
Недостатки:
- Недостаточная наглядность.
- Необходимость производить подчас очень громоздкие вычисления.
Табличный способ
При табличном задании функции просто выписывается ряд значений независимой переменной и соответствующие им значения функции.
Пример:

Преимущество:
Для каждого значения независимой переменной, входящей в таблицу, сразу можно найти соответствующее значение функции.
Недостатки:
- При нем, чаще всего, невозможно задать функцию полностью;
- Недостаточная наглядность.
Графический способ
Введем определение графика функции:
График функции $f(x)$ называется множество всех точек декартовой координатной плоскости вида $(x,\ f\left(x\right))$, где $x\in D$.
Задание графика функции называется графическим способом задания функции $f(x)$.
Пример: рис. 1.
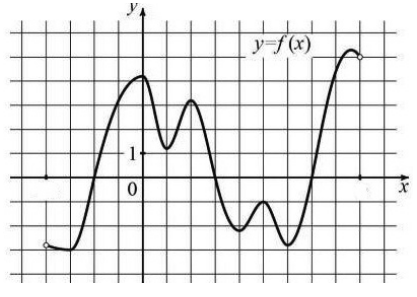
Рис. 1. График функции $y=f(x)$.
Схема для построения графика функции
- Область определения $D(f)$ и область значения $E(f)$.
- Четность ($f\left(x\right)=f\left(-x\right))$, нечетность ($f\left(x\right)=-f\left(x\right))$, периодичность ($f\left(x\right)=f\left(x+T\right))$.
- Точки пересечения с осями координат и промежутки, где $f\left(x\right)>0$ и $f\left(x\right)
- Исследовать на возрастание ${(f}'\left(x\right)>0)$, убывание ${(f}'\left(x\right)
- Исследовать на точки перегиба и интервалы выпуклости $(f^{''}\left(x\right) > 0)$, вогнутости ($f^{''}\left(x\right)
- Вычислить пределы на границах области определения.
- Значения в дополнительных точках.
- График.
Правила построения графиков
- $y=f(x-a)$ получается из графика $f(x)$ сдвигом вдоль оси $Ox$ на $|a|$ вправо, если $a > 0$ и влево, если $a
- $y=f\left(x\right)+b$ получается из графика $f(x)$ сдвигом вдоль оси $Oy$ на $|b|$ вверх, если $b>0$ и вниз, если $\ b
- $y=f(kx)$ получается из графика $f(x)$ сжатием к оси $Oy$, если $k>1$ и растяжением, если $0
- $y=kf(x)$ получается из графика $f(x)$ растяжением от оси $Ox$ в $k$ раз, если $k > 1$ и сжатием к оси $Ox$ в $\frac{1}{k}$ раз, если $0
- $y=f(-x)$ получается из графика $f(x)$ симметричным отображением относительно оси $Oy$.
- $y=-f(x)$ получается из графика $f(x)$ симметричным отображением относительно оси $Ox$.
- $y=|f\left(x\right)|$ получается из графика $f(x)$ следующим образом: часть графика $f(x)$,лежащая над осью $Ox$ остается неизменна, а лежащая под $Ox$ отображается симметрично относительно оси $Oy$.
- $y=f\left(|x|\right)$ получается из графика $f(x)$ следующим образом: часть графика $f(x)$,лежащая справа от оси $Oy$ остается неизменна, а затем эта часть отображается симметрично относительно оси $Oy$, заменяя часть, лежащую слева от $Oy$.
Пример исследования и построения функции
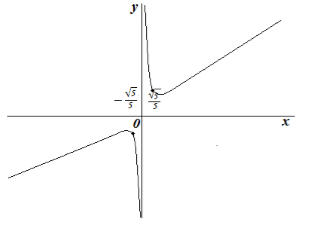
Исследовать функцию и построить её график:
\[y=\frac{5x^2+x+1}{x}\]- Область определения: $\left(-\infty ,0\right)(0,\infty )$. Область значения:$\left(-\infty ,1-2\sqrt{5}\right][1+2\sqrt{5},\infty )$
- функция ни четна, ни нечетна, непериодическая.
- Точек пересечения с осями координат нет.
- $y'=\frac{10x^2+x-5x^2-x-1}{x^2}=\frac{5x^2-1}{x^2}$ \[\frac{5x^2-1}{x^2}=0\] \[x\ne 0,\ x=\pm \frac{\sqrt{5}}{5}\]
- $y^{''}=\frac{{10x}^3-{10x}^3+2x}{x^4}=\frac{2}{x^3}$ \[\frac{2}{x^3}=0\] \[x\ne 0\]
- ${\mathop{lim}_{x\to 0-0} y\ }=-\infty $, ${\mathop{lim}_{x\to 0+0} y\ }=+\infty $, ${\mathop{lim}_{x\to -\infty } y\ }=-\infty $, ${\mathop{lim}_{x\to +\infty } y\ }=+\infty $
При $x\in \left(-\infty ,0\right)$ функция отрицательна, при $x\in \left(0,\infty \right)$ функция положительна.
Методом интервалов получаем, что
Функция возрастает при $x\in \left(-\infty ,-\frac{\sqrt{5}}{5}\right)\left(\frac{\sqrt{5}}{5},\infty \right)$ и убывает при $x\in \left(-\frac{\sqrt{5}}{5},0\right)\left(0,\frac{\sqrt{5}}{5}\right)$
Максимум функции: $\left(-\frac{\sqrt{5}}{5},1-2\sqrt{5}\right)$
Минимум функции: $\left(\frac{\sqrt{6}}{6},1+2\sqrt{5}\right)$
Методом интервалов получаем, что функция выпукла при $x\in \left(0,\infty \right)$ и вогнута при $x\in \left(-\infty ,0\right)$