Достаточно часто на практике приходится иметь дело с функциями, которые определены не на всей числовой прямой, либо принимают не любые значения из множества действительных чисел.
В таких случаях при построении графиков функций получаем, что график функции не является непрерывной линией, а имеет некоторые разрывы. В результате чего становится целесообразным ввести понятие «асимптота».
Асимптота -- это такая прямая, к которой график заданной функции приближается сколько угодно близко, но не пересекает ее.
Среди асимптот выделяют следующие виды:
- вертикальная асимптота (параллельна оси ОY);
- горизонтальная асимптота (параллельна оси ОХ);
- наклонная асимптота (расположена под углом к осям координат).
Отметим, что асимптоты на графике функции изображаются пунктирной линией.
Вертикальная асимптота -- это прямая, определяемая уравнением $x=a$, для которой выполняются условия $\mathop{\lim }\limits_{x\to a\pm 0} f(x)=\infty $ или $\mathop{\lim }\limits_{x\to a} f(x)=\infty $.
Вертикальная асимптота может быть только в точках разрыва функции $y=f(x)$, т.е. в тех точках, где данная функция неопределенна.
Найти вертикальную асимптоту графика данной функции: $y=\frac{5}{x-2} $.
Решение:
Область определения функции: $D_{y} =\{ x\in R|x\ne 2\} $.
\[\mathop{\lim }\limits_{x\to 2} \frac{5}{x-2} =\frac{5}{0} =\infty \]Следовательно, прямая $x=2$ является вертикальной асимптотой (см. рис.).
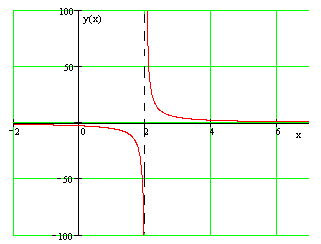
Рисунок 1.
Горизонтальная асимптота -- это прямая, определяемая уравнением $y=b$, для которой выполняются условия $\mathop{\lim }\limits_{x\to \pm \infty } f(x)=b$.
Найти горизонтальную асимптоту графика данной функции: $y=5^{x} $.
Решение:
\[\mathop{\lim }\limits_{x\to -\infty } 5^{x} =0;\mathop{\lim }\limits_{x\to +\infty } 5^{x} =\infty \]Следовательно, прямая $y=0$ является горизонтальной асимптотой (см. рис.).
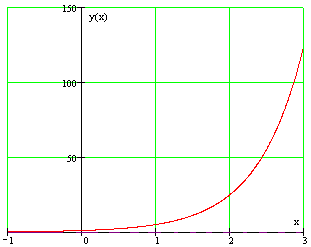
Рисунок 2.
График функции может иметь только правую либо только левую горизонтальную асимптоту.
Наклонная асимптота -- это прямая, определяемая уравнением $y=kx+b$, для которой выполняется условие $\mathop{\lim }\limits_{x\to \infty } [f(x)-kx+b]=0$.
Условия существования наклонной асимптоты определяются следующей теоремой.
Если функция $y=f(x)$ имеет конечные пределы $\mathop{\lim }\limits_{x\to \infty } \frac{f(x)}{x} =k;\mathop{\lim }\limits_{x\to \infty } [f(x)-kx]=b$, то данная функция имеет наклонную асимптоту, заданную уравнением $y=kx+b$ при $x\to \infty $.
Наклонная асимптота может быть левой (график приближается справа), правой (график приближается слева) или двусторонней (график приближается с обоих сторон).
Найти наклонную асимптоту графика данной функции: $y=\frac{x^{2} }{x-2} $.
Решение:
\[k=\mathop{\lim }\limits_{x\to \infty } \frac{f(x)}{x} =\mathop{\lim }\limits_{x\to \infty } \frac{x^{2} }{x(x-2)} =\mathop{\lim }\limits_{x\to \infty } \frac{x^{2} }{x^{2} -2x} =\mathop{\lim }\limits_{x\to \infty } \frac{1}{1-2/x} =\frac{1}{1-0} =1;\] \[\begin{array}{l} {b=\mathop{\lim }\limits_{x\to \infty } [f(x)-kx]=\mathop{\lim }\limits_{x\to \infty } \left[\frac{x^{2} }{x-2} -x\right]=\mathop{\lim }\limits_{x\to \infty } \frac{x^{2} -x(x-2)}{x-2} =\mathop{\lim }\limits_{x\to \infty } \frac{x^{2} -x^{2} +2x}{x-2} =\mathop{\lim }\limits_{x\to \infty } \frac{2x}{x-2} =} \\ {=\mathop{\lim }\limits_{x\to \infty } \frac{2}{1-2/x} =\frac{2}{1-0} =2} \end{array}\]Следовательно, прямая $y=x+2$ является наклонной асимптотой (см. рис.). В данном случае имеем двустороннюю наклонную асимптоту.
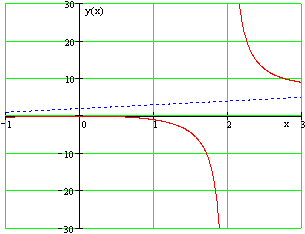
Рисунок 3.
Найти наклонную асимптоту графика данной функции: $y=\frac{x^{4} }{x-2} $.
Решение:
\[k=\mathop{\lim }\limits_{x\to \infty } \frac{f(x)}{x} =\mathop{\lim }\limits_{x\to \infty } \frac{x^{4} }{x(x-2)} =\mathop{\lim }\limits_{x\to \infty } \frac{x^{4} }{x^{2} -2x} =\mathop{\lim }\limits_{x\to \infty } \frac{1}{1/x^{2} -2/x^{3} } =\frac{1}{0-0} =\infty \]Следовательно, график данной функции не имеет наклонной асимптоты.
График функции может иметь одновременно несколько асимптот, например, вертикальную и наклонную.
Найти асимптоты графика данной функции: $y=\frac{3x^{2} }{x-1} $.
Решение:
Область определения функции: $D_{y} =\{ x\in R|x\ne 1\} $.
\[\mathop{\lim }\limits_{x\to 1} \frac{3x^{2} }{x-1} =\infty \]Следовательно, прямая $x=1$ является вертикальной асимптотой (см. рис.).
\[k=\mathop{\lim }\limits_{x\to \infty } \frac{f(x)}{x} =\mathop{\lim }\limits_{x\to \infty } \frac{3x^{2} }{x(x-1)} =\mathop{\lim }\limits_{x\to \infty } \frac{3x^{2} }{x^{2} -x} =\mathop{\lim }\limits_{x\to \infty } \frac{3}{1-1/x} =\frac{3}{1-0} =3;\] \[\begin{array}{l} {b=\mathop{\lim }\limits_{x\to \infty } [f(x)-kx]=\mathop{\lim }\limits_{x\to \infty } \left[\frac{3x^{2} }{x-1} -3x\right]=\mathop{\lim }\limits_{x\to \infty } \frac{3x^{2} -3x(x-1)}{x-1} =\mathop{\lim }\limits_{x\to \infty } \frac{3x^{2} -3x^{2} +3x}{x-1} =\mathop{\lim }\limits_{x\to \infty } \frac{3x}{x-1} =} \\ {=\mathop{\lim }\limits_{x\to \infty } \frac{3}{1-1/x} =\frac{3}{1-0} =3} \end{array}\]Следовательно, прямая $y=3x+3$ является наклонной асимптотой (см. рис.). В данном случае имеем двустороннюю наклонную асимптоту.
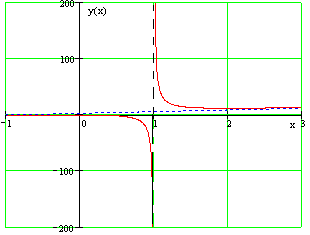
Рисунок 4.












