Понятие синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника
Будем измерять величины углов в радианах. Поворот координатной плоскости вокруг начала координат на угол $\alpha $ радиан будем обозначать символом $R^{\alpha }$.
Через $P_{\alpha }$ будем обозначать точку единичной окружности $x^2+y^2=1$ которая получается из точки $P_0$ с координатами $(1,0)$ путем поворота плоскости вокруг начала координат на угол $\alpha $.
Рассмотрим в Декартовой системе координат окружность с радиусом $R >0$ и центром $(0,0)$ (рис. 1).
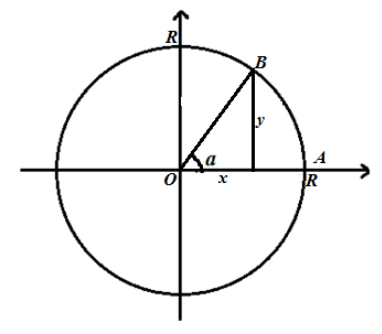
Рисунок 1. Окружность радиуса $R >0$.
$\left[OB\right]$ получается из $\left[OA\right]=R$ путем поворота на угол $\alpha $ радиан. Пусть $x$ и $y$ абсцисса и ордината точки $B$, соответственно, тогда
Так как в определениях синуса и косинуса их значения не зависят от радиуса окружности, то можно принять $R=1$. Поэтому, другим способом, тригонометрические значения определяются следующим образом:
Синусом острого угла называется ордината единичной окружности, которая получается из точки $(1,\ 0)$ путем поворота на угол $\alpha $ радиан.
Косинусом острого угла называется абсцисса единичной окружности, которая получается из точки $(1,\ 0)$ путем поворота на угол $\alpha $ радиан.
Тангенсом угла называется отношение значения синуса этого угла к значению косинуса этого угла.
Котангенсом угла называется отношение значения косинуса этого угла к значению синуса этого угла.
Основное тригонометрическое тождество
Проверим следующее тождество:
\[{sin}^2A+{cos}^2A=1\]Для этого будем рассматривать прямоугольный треугольник $ABC$ c прямым углом $C$ (рис. 2).
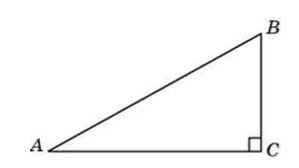
Рисунок 2.
Из него получим
\[{\left(\frac{BC}{AB}\right)}^2+{\left(\frac{AC}{AB}\right)}^2=\frac{{BC}^2+{AC}^2}{{AB}^2}\]Из теоремы Пифагора мы знаем, что ${BC}^2+{AC}^2={AB}^2$, следовательно
\[{sin}^2A+{cos}^2A=\frac{{BC}^2+{AC}^2}{{AB}^2}=\frac{{AB}^2}{{AB}^2}=1\]Это тождество называется основным тригонометрическим тождеством.
Основные значения синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника
Вычислим значения для углов в ${30}^{{}^\circ },\ {45}^{{}^\circ }$ и ${60}^{{}^\circ }$. Для этого вспомним следующую теорему.
Катет, лежащий напротив угла в ${30}^{{}^\circ }$, равняется половине гипотенузы прямоугольного треугольника.
Пусть для начала у нас $\angle A={30}^{{}^\circ }$. Так как треугольник прямоугольный, то $\angle B={60}^{{}^\circ }$.
По теореме 1, имеем $AB=2BC$.
Используя основное тригонометрическое тождество (5), получим:
Теперь нетрудно найти тангенсы и котангенсы этих углов.
Пусть теперь $\angle A={45}^{{}^\circ }$. Тогда $\angle B={45}^{{}^\circ }$, то есть прямоугольный треугольник -- равнобедренный. По теореме Пифагора ${BC}^2+{AC}^2={AB}^2$, следовательно, ${AB}^2={2BC}^2=2{AC}^2$, то есть
Тогда
Сведем все полученные данные в таблицу (таблица 1).
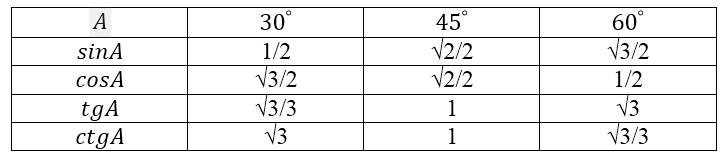
Рисунок 3.
Пример задачи
Найти все тригонометрические значения угла $A$, если$AB=25,\ BC=20,\ AC=15.$
Решение.
Все решение задачи будем производить с помощью прямоугольного треугольника (рис. 2).
\[sinA=\frac{BC}{AB}=\frac{20}{25}=0,8\] \[cosA=\frac{AC}{AB}=\frac{15}{25}=0,6\] \[tgA=\frac{BC}{AC}=\frac{20}{15}=1\frac{1}{3}\] \[ctgA=\frac{AC}{BC}=\frac{15}{20}=0,75\]











