Соотношения между сторонами и углами треугольника

Источник статьи

Автор24 — учеба по твоим правилам

Введем сначала определение треугольника.

Определение 1

Треугольником называется геометрическая фигура, состоящая из трех отрезков, вершинами которых являются три точки, не лежащие на одной прямой (рис. 1).

Отрезки называются при этом сторонами треугольника, а концы отрезков - вершинами треугольника.

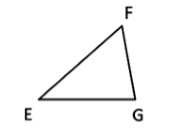
Рисунок 1. Треугольник

Сумма углов треугольника

Рассмотрим теорему о сумме углов треугольника.

Теорема 1

Сумма углов любого треугольника равна ${180}^0.$

Доказательство.

Пусть нам дан произвольный треугольник $ABC$ . Докажем, что сумма его углов равна ${180}^0$ . Построим прямую $a||AC$ (рис. 2)

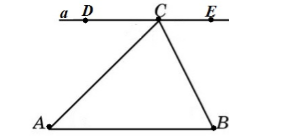
Рисунок 2. Иллюстрация теоремы 1

Так как $a||AC$ , то $\angle A=\angle ACD,\ \angle B=\angle BCE$ как накрест лежащие углы при параллельных прямых и секущих $AC$ и $BC$ , соответственно.

Так как $\angle DCE$ -- развернутый, то он равен ${180}^0$ .

Получаем

То есть

Теорема доказана.

Теорема о соотношении между сторонами и углами треугольника

Перед тем, как ввести следующую теорему, введем понятие внешнего угла треугольника.

Определение 2

Внешний угол треугольника -- угол, смежный с углом треугольника (рис. 3).

Введем теорему о внешнем угле треугольника:

Теорема 2

Внешний угол треугольника равен сумме двух не смежных с ним углов треугольника.

«Соотношения между сторонами и углами треугольника» 👇

Помощь эксперта по теме работы

Найти эксперта

Решение задач от ИИ за 2 минуты

Решить задачу

Помощь с рефератом от нейросети

Написать ИИ

Доказательство.

Пусть нам дан произвольный треугольник $ABC$ . Рассмотрим внешний угол треугольника $\angle BCD$ (рис. 3).

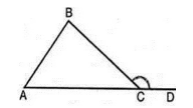
Рисунок 3. Внешний угол треугольника

По теореме 1 $\angle A+\angle C+\angle B={180}^0$ , то есть $\angle C={180}^0-(\angle A+\angle B)$ .

С другой стороны

Теорема доказана.

Теорема 3

В любом треугольнике:

Против большей стороны лежит больший угол.
Против большего угла лежит большая сторона.

Доказательство.

Пусть нам дан произвольный треугольник $ABC$ , такой, что сторона $AB>AC$ . Докажем, что угол $\angle C>\angle B$ .

Построим на стороне $AB$ отрезок $AD=AC$ (рис. 4).

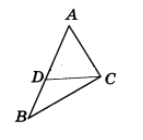
Рисунок 4. Иллюстрация теоремы 3

Очевидно, что отрезок $CD$ лежит внутри треугольника $ABC$ . Угол $ADC$ - внешний угол треугольника $BDC$ , следовательно, по теореме 2, $\angle ADC >\angle B$ . Так как $AD=AC$ , то треугольник $DCA$ - равнобедренный. Следовательно, $\angle ADC=\angle DCA$ , значит $\angle DCA>\angle B$ . Получаем

$∠ C > ∠ D C A > ∠ B$
$\angle C >\angle DCA >\angle B$
Пусть нам дан произвольный треугольник $ABC$ , такой, что $\angle C>\angle B$ . Докажем, что $AB>AC$ .

Предположим противное, что $\ AB\le AC$ . Рассмотрим два случая:
- $AB
Тогда по первому пункту этой теоремы $\angle B >\angle C$ . Противоречие.
- $AB=AC$ .
Тогда треугольник $ABC$ равнобедренный, и, следовательно, $\angle B=\angle C$ . Противоречие.

Значит $AB >AC$ .

Теорема доказана.

Неравенство треугольника

Теорема 4

Любая сторона треугольника меньше суммы двух других сторон.

Доказательство.

Пусть нам дан произвольный треугольник $ABC$ . Докажем, что$AB

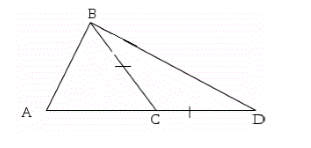
Рисунок 5. Иллюстрация теоремы 4

Так как $CD=BC$ , то треугольник $BCD$ равнобедренный, следовательно, $\angle CBD=\angle D$ . Тогда $\angle ABD >\angle D$ . Значит $AD >AB$ . Так как