Предварительные сведения
Для начала введем сведения и обозначения, которые будут необходимы нам в дальнейшем.
Будем рассматривать треугольник $ABC$ с острыми углами $A$ и $C$. Проведем в нем высоту $BH$. Введем следующие обозначения: $AB=c,\ BC=a,\ $$AC=b,\ AH=x,\ BH=h\ $(рис. 1).
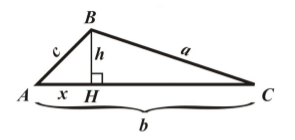
Рисунок 1.
Введем без доказательств теорему о площади треугольника.
Площадь треугольника определяется как половина произведения длины его стороны, на высоту, проведенную к ней, то есть
\[S=\frac{1}{2}bh\]Формула Герона
Введем и докажем теорему о нахождении площади треугольника по трем известным сторонам. Эта формула носит название формулы Герона.
Пусть нам даны три стороны треугольника $a,\ b\ и\ c$. Тогда площадь этого треугольника выражается следующим образом
\[S=\sqrt{p\left(p-a\right)\left(p-b\right)(p-c)}\]где $p$ - полупериметр данного треугольника.
Доказательство.
Будем пользоваться обозначениями, введенными на рисунке 1.
Рассмотрим треугольник $ABH$. По теореме Пифагора, получим
\[h^2=c^2-x^2\]Очевидно, что $HC=AC-AH=b-x$
Рассмотрим треугольник $\ CBH$. По теореме Пифагора, получим
\[h^2=a^2-{HC}^2\] \[h^2=a^2-{(b-x)}^2\] \[h^2=a^2-b^2+2bx-x^2\]Приравняем значения квадрата высоты из двух полученных соотношений
\[c^2-x^2=a^2-b^2+2bx-x^2\] \[2bx=c^2-a^2+b^2\] \[x=\frac{c^2-a^2+b^2}{2b}\]Из первого равенства найдем высоту
\[h^2=c^2-{\left(\frac{c^2-a^2+b^2}{2b}\right)}^2\] \[h^2=\frac{{4b^2c}^2-{\left(c^2-a^2+b^2\right)}^2}{4b^2}\] \[h^2=\frac{\left(2bc-c^2+a^2-b^2\right)({2bc+c}^2-a^2+b^2)}{4b^2}\] \[h^2=\frac{\left(a^2-{\left(c-b\right)}^2\right)({\left(c+b\right)}^2-a^2)}{4b^2}\] \[h^2=\frac{\left(a-c+b\right)\left(a+c-b\right)\left(c+b-a\right)(c+b+a)}{4b^2}\] \[h^2=\frac{(a+b+c)\left(a+b+c-2c\right)\left(a+b+c-2b\right)\left(a+b+c-2a\right)}{4b^2}\]Так как полупериметр равен $p=\frac{a+b+c}{2}$, то есть $a+b+c=2p$, то
\[h^2=\frac{2p\left(2p-2c\right)\left(2p-2b\right)\left(2p-2a\right)}{4b^2}\] \[h^2=\frac{4p\left(p-a\right)\left(p-b\right)\left(p-c\right)}{b^2}\] \[h=\sqrt{\frac{4p\left(p-a\right)\left(p-b\right)\left(p-c\right)}{b^2}}\] \[h=\frac{2}{b}\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\]По теореме 1, получим
\[S=\frac{1}{2}bh=\frac{b}{2}\cdot \frac{2}{b}\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\]Теорема доказана.
Примеры задач на использование формулы Герона
Найти площадь треугольника, если его стороны равняются $3$ см, $6$ см и $7$ см.
Решение.
Найдем вначале полупериметр этого треугольника
\[p=\frac{3+6+7}{2}=\frac{16}{2}=8\ см\]По теореме 2, получим
\[S=\sqrt{8\left(8-3\right)\left(8-6\right)\left(8-7\right)}=\sqrt{8\cdot 5\cdot 2\cdot 1}=4\sqrt{5}\]Ответ: $4\sqrt{5}$.
Найти площадь параллелепипеда, со сторонами $8$ см и $5$ см и меньшей диагональю, равной $5$ см.
Решение.
Пусть нам дан параллелограмм $ABCD$, где $AD=8\ см,\ AB=5\ см\ и\ BD=5\ см$ (рис. 2).
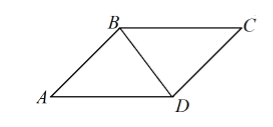
Рисунок 2.
Так как диагональ параллелограмма является его осью симметрии, то треугольники $ABD$ и $BDC$ равны между собой. Следовательно
\[S=S_{ABD}+S_{BDC}=2S_{ABD}\]Полупериметр треугольника $ABD$ равен
\[p=\frac{5+5+8}{2}=\frac{18}{2}=9\ см\]По теореме 2
\[S_{ABD}=\sqrt{9\left(9-5\right)\left(9-5\right)\left(9-8\right)}=\sqrt{9\cdot 4\cdot 4\cdot 1}=12\]Следовательно
\[S=2\cdot 12=24\]Ответ: $24$.













