Понятие окружности
Окружность -- геометрическая фигура, состоящая из всех точек, расположенных на равном расстоянии от заданной точки.
В рамках определения 1, заданная точка называется центром окружности.
Отрезок, соединяющий центр окружности с любой ее точкой называется радиусом окружности $(r)$ (Рис. 1).
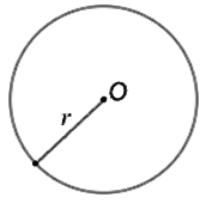
Рисунок 1. Окружность с центром в точке $O$ и радиусом $r$
Уравнение окружности
Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ -- произвольная точка этой окружности (рис. 2).
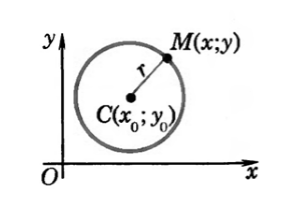
Рисунок 2. Окружность в декартовой системе координат
Расстояние от центра окружности до точки $M$ вычисляется следующим образом
Но, так как $M$ лежит на окружности, то по определению 3, получаем $CM=r$. Тогда получим следующее
Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.
В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид
Длина окружности
Выведем формулу длины окружности $C$ через её радиус. Для этого рассмотрим две окружности с длинами $C$ и $C'$ и радиусами $R$ и $R'$. Впишем в ним правильные $n-угольники$ с периметрами $P$ и $P'$ и длинами сторон $a$ и $a'$ соответственно. Как нам известно, сторона вписанного -угольника равна
Тогда, получим
Следовательно
Неограниченно увеличивая количество сторон правильных многоугольников $n$ получим, что
Отсюда, получаем
То есть
Получили, что отношение длины окружности к её диаметру постоянное число для любой окружности. Эту константу принято обозначать числом $\pi \approx 3,14$. Таким образом, получим
Формула (2) и есть формула для вычисления длины окружности.
Площадь круга
Круг -- часть плоскости, ограниченной окружностью.
Выведем формулу для вычисления площади круга.
Рассмотрим следующую ситуацию. Пусть нам дана окружность с радиусом $R$. Обозначим её площадь через $S$. В нее вписан правильный -угольник с площадью $S_n$, в который, в свою очередь вписана окружность с площадью ${S'}_n$ (рис. 3).
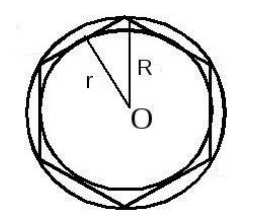
Рисунок 3.
Из рисунка очевидно, что
Используем следующую известную формулу для правильного многоугольника:
Будем теперь неограниченно увеличивать число сторон правильного многоугольника. Тогда, при $n\to \infty $, получим
Тогда
По формуле, площадь правильного многоугольника равна $S_n=\frac{1}{2}P_nr$, $P_n\to 2\pi R$, следовательно
Формула (3) и есть формула для вычисления площади круга.
Пример задачи на понятие окружности
Найти уравнение окружности с центром в точке $(1,\ 1)$. проходящей через начало координат, найти длину данной окружности и площадь круга, ограниченного данной окружностью.
Решение.
Найдем сначала уравнение данной окружности. Для этого будем использовать формулу (1). Так как центр окружности лежит в точке $(1,\ 1)$, получим
\[{(x-1)}^2+{(y-1)}^2=r^2\]Найдем радиус окружности как расстояние от точки $(1,\ 1)$ до точки $(0,0)$
\[r=\sqrt{{(1-0)}^2+{(1-0)}^2}=\sqrt{2}\]Получаем, уравнение окружности имеет вид:
\[{(x-1)}^2+{(y-1)}^2=2\]Найдем длину окружности по формуле (2). Получим
\[C=2\pi r=2\sqrt{2}\pi \]Найдем площадь по формуле (3)
\[S=\pi r^2=2\pi \]Ответ: ${(x-1)}^2+{(y-1)}^2=2$, $C=2\sqrt{2}\pi $, $S=2\pi $











