Уравнение линии на плоскости
Введем для начала понятие уравнения линии в двумерной системе координат. Пусть в декартовой системе координат построена произвольная линия $L$ (Рис. 1).
Рисунок 1. Произвольная линия в системе координат
Уравнение с двумя переменными $x$ и $y$ называется уравнением линии $L$, если этому уравнению удовлетворяют координаты любой точки, принадлежащей линии $L$ и не удовлетворяет ни одна точка, не принадлежащая линии $L.$
Уравнение окружности
Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ -- произвольная точка этой окружности (рис. 2).
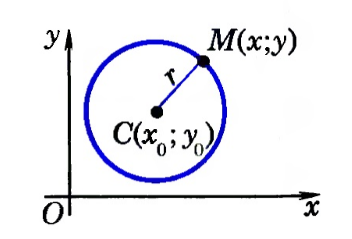
Рисунок 2. Окружность в декартовой системе координат
Расстояние от центра окружности до точки $M$ вычисляется следующим образом
Но, так как $M$ лежит на окружности, то получаем $CM=r$. Тогда получим следующее
Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.
В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид
Выведем уравнение прямой $l$ в декартовой системе координат $xOy$. Пусть точки $A$ и $B$ имеют координаты $\left\{x_1,\ y_1\right\}$ и $\{x_2,\ y_2\}$ соответственно, причем точки $A$ и $B$ выбраны так, что прямая $l$ - серединный перпендикуляр к отрезку $AB$. Выберем произвольную точку $M=\{x,y\}$, принадлежащую прямой $l$ (рис. 3).
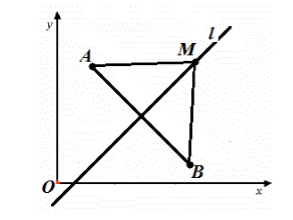
Рисунок 3. Прямая в декартовой системе координат
Так как прямая $l$ - серединный перпендикуляр к отрезку $AB$, то точка $M$ равноудалена от концов этого отрезка, то есть $AM=BM$.
Найдем длины данных сторон по формуле расстояния между точками:
Следовательно
Обозначим через $a=2\left(x_1-x_2\right),\ b=2\left(y_1-y_2\right),\ c={x_2}^2+{y_2}^2-{x_1}^2-{y_1}^2$, Получаем, что уравнение прямой в декартовой системе координат имеет следующий вид:
Здесь можно выделить два частных случая для уравнения прямой. Пусть прямая $l$ проходит через точку $M=\{x_0,y_0\}$, тогда
-
Если прямая $l$ параллельна оси $Ox$, то она имеет вид
\[y=y_0\] -
Если прямая $l$ параллельна оси $Oy$, то она имеет вид
\[x=x_0\]
Пример задачи на нахождение уравнений линий в декартовой системе координат
Найти уравнение окружности с центром в точке $(2,\ 4)$. Проходящей через начало координат и прямую, параллельную оси $Ox,$ проходящей через её центр.
Решение.
Найдем сначала уравнение данной окружности. Для этого будем использовать общее уравнение окружности (выведенное выше). Так как центр окружности лежит в точке $(2,\ 4)$, получим
\[{(x-2)}^2+{(y-4)}^2=r^2\]Найдем радиус окружности как расстояние от точки $(2,\ 4)$ до точки $(0,0)$
\[r=\sqrt{{(2-0)}^2+{(4-0)}^2}=\sqrt{20}=2\sqrt{5}\]Получаем, уравнение окружности имеет вид:
\[{(x-2)}^2+{(y-4)}^2=20\]Найдем теперь уравнение окружности, используя частный случай 1. Получим
\[y=4\]













