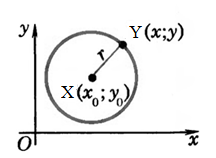Очевидно, что границей любого круга является окружность. Поэтому понятие периметра круга совпадает с таким понятием, как длина окружности. Поэтому вначале вспомним, что является окружностью, и какие понятия с ней связаны.
Понятие окружности
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Центром окружности будем называть точку, которая задается в рамках определения 1.
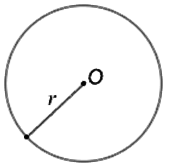
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки (Рис. 1).
В декартовой системе координат $xOy$ мы также можем ввести уравнение любой окружности. Обозначим центр окружности точкой $X$, которая будет иметь координаты $(x_0,y_0)$. Пусть радиус этой окружности равняется $τ$. Возьмем произвольную точку $Y$, координаты которой обозначим через $(x,y)$ (рис. 2).
По формуле расстояния между двумя точками в заданной нами системе координат, получим:
$|XY|=\sqrt{(x-x_0)^2+(y-y_0)^2}$
С другой стороны, $|XY|$ - это расстояние от любой точки окружности до выбранного нами центра. То есть, по определению 3, получим, что $|XY|=τ$, следовательно
$\sqrt{(x-x_0)^2+(y-y_0)^2}=τ$
$(x-x_0)^2+(y-y_0)^2=τ^2$ (1)
Таким образом, мы и получаем, что уравнение (1) является уравнением окружности в декартовой системе координат.
Длина окружности (периметр круга)
Будем выводить длину произвольной окружности $C$ с помощью её радиуса, равного $τ$.
Будем рассматривать две произвольные окружности. Обозначим их длины через $C$ и $C'$, у которых радиусы равняются $τ$ и $τ'$. Будем вписывать в эти окружности правильные $n$-угольники, периметры которых равняются $ρ$ и $ρ'$, длины сторон которых равняются $α$ и $α'$, соответственно. Как мы знаем, сторона вписанного в окружность правильного $n$ – угольника равняется
$α=2τsin\frac{180^0}{n}$
Тогда, будем получать, что
$ρ=nα=2nτ\frac{sin180^0}{n}$
$ρ'=nα'=2nτ'\frac{sin180^0}{n}$
Значит
$\frac{ρ}{ρ'}=\frac{2nτsin\frac{180^0}{n}}{2nτ'\frac{sin180^0}{n}}=\frac{2τ}{2τ'}$
Получаем, что отношение $\frac{ρ}{ρ'}=\frac{2τ}{2τ'}$ будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
$\lim_{n\to\infty}(\frac{ρ}{ρ'})=\frac{2τ}{2τ'}$
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть $n→∞$), будем получать равенство:
$lim_{n\to\infty}(\frac{ρ}{ρ'})=\frac{C}{C'}$
Из последних двух равенств получим, что
$\frac{C}{C'}=\frac{2τ}{2τ'}$
То есть
$\frac{C}{2τ}=\frac{C'}{2τ'}$
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
$\frac{C}{2τ}=const$
Эту постоянную принять называть числом «пи» и обозначать $π$. Приближенно, это число будет равняться $3,14$ (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
$\frac{C}{2τ}=π$
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
$C=2πτ$
Пример задач
Найти периметр круга, который вписан в квадрат со стороной, равной $α$.
Решение.
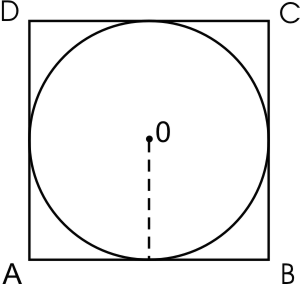
Пусть нам дан квадрат $ABCD$, в который вписана окружность с центром $O$. Изобразим рисунок по условию задачи (рис. 3).
Очевидно, что центр окружности будет совпадать с центром квадрата, в которой она вписана. Так как квадрат описан вокруг окружности, то его стороны будут касательными к ней, то есть радиус, проведенный, к примеру, к стороне $AB$ будет перпендикулярен к ней. Значит, диаметр окружности равняется стороне квадрата. То есть
$τ=\frac{α}{2}$
По формуле периметра круга, получим, что
$C=2π\cdot \frac{α}{2}=πα$
Ответ: $πα$.
Найти периметр круга, который описан у прямоугольного треугольника с катетами, равными $α$ и $β$.
Решение.
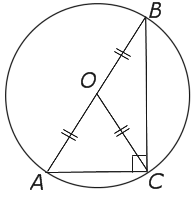
Пусть нам дан треугольник $ABC$ с прямым углом $C$, у которой описана окружность с центром $O$. Как мы знаем, диаметром такой окружности является гипотенуза такого треугольника. То есть $|AO|=|OB|=|OC|=τ$ (рис. 4).
По теореме Пифагора, гипотенуза равняется
$|AB|=\sqrt{α^2+β^2}$
То есть
$|AO|=τ=\frac{\sqrt{α^2+β^2}}{2}$
Периметр круга, по формуле, равняется
$C=2π\cdot \frac{\sqrt{α^2+β^2}}{2}=π\sqrt{α^2+β^2}$
Ответ: $π\sqrt{α^2+β^2}$.