Определение призмы
Призмой называется многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани - параллелограммами, имеющими общие стороны с этими многоугольниками. Эти параллелограммы называются боковыми гранями призмы, а оставшиеся два многоугольника называются её основаниями.
Призма является частным случаем цилиндра. Параллелепипед является частным случаем призмы.
Призма обладает следующим свойством:
Любое сечение призмы плоскостью, параллельной её основанию, делит данную призму на две призмы так, что отношение боковых поверхностей и отношение объёмов этих призм равно отношению длин их боковых рёбер. Любое сечение призмы плоскостью, параллельной её боковому ребру, делит данную призму на две призмы так, что отношение объёмов этих призм равно отношению длин их боковых рёбер. Любое сечение призмы плоскостью, параллельной её боковому ребру, делит данную призму на две призмы так, что отношение объёмов этих призм равно отношению площадей их основания.
Виды призм
-
Прямая призма. Боковые рёбра прямой призмы перпендикулярны плоскости основания.
-
Наклонная призма. Боковые рёбра наклонной призмы находятся относительно плоскости основания под углом, отличным от $90^\circ$.
-
Правильная призма. Основанием прямой призмы является правильный многоугольник. Её боковые гран -- равные прямоугольники.
Полуправильным многогранником называется правильная призма, боковые грани которой -- квадраты.
Объём прямой призмы
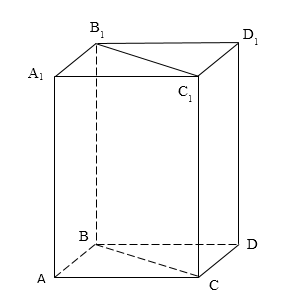
Для вывода формулы вычисления объёма правильной призмы возьмём призму, в основании которой лежит треугольник. Достроим её до прямоугольного параллелепипеда (рисунок 1).
 Тетраэдр, достроенный до параллелепипеда">
Тетраэдр, достроенный до параллелепипеда">
Рисунок 1. Тетраэдр, достроенный до параллелепипеда
Из предыдущей главы мы знаем, что объём прямоугольного параллелепипеда равен:
где
Т.к. полученный параллелепипед состоит из исходной призмы и призмы, равной ей по объёму, то объём исходной призмы будет равен
Т.к.
где $a$, $b$, $c$ длины сторон $AB$, $BC$, $AC$ соответственно, и их произведение равно площади основания исходной призмы, то запишем в общем виде формулу нахождения объёма прямой призмы:
где $S_{осн.}$ -- площадь основания призмы, $H$ -- высота, проведённая к основанию призмы.
Данная формула верна для прямой призмы с любым многоугольником в основании.
Объём наклонной призмы
Для вывода формулы нахождения объёма наклонной призмы рассмотрим треугольную наклонную призму $ABCDFE$. Проведём через ребро $DC$ плоскость $\alpha $, перпендикулярную основанию $ABCD$ исходной призмы, и построим треугольную усечённую призму (рисунок 2).
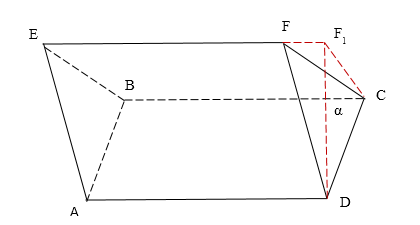
Рисунок 2. Наклонная призма, плоскость $\alpha $
Теперь через ребро $AB$ проведём плоскость $\beta $, параллельную плоскости $\alpha $ (рисунок 3).
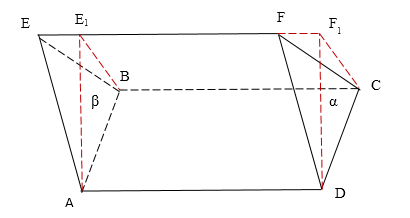
Рисунок 3. Наклонная призма, плоскости $\alpha $ и $\beta $
Если применить такое преобразования к наклонным граням ещё раз, то получится призма, у которой все боковые грани перпендикулярны основанию. Снова получился прямая призма.
Если её подвергнуть подобному преобразованию (сначала дополнить первой усечённой призмой, затем отсечь вторую усечённую призму), то достроенная и отсекаемая призмы совмещаются параллельным переносом на отрезок $AB$. Из этого следует, что фигуры имеют одинаковый объём.
Следовательно, объём построенной прямой призмы равен объёму исходной наклонной.
Объём наклонной призмы равен произведению площади основания на высоту:
Вывод
Объём любой призмы (наклонной и прямой) находится по формуле:
где $a\cdot b$ - площадь основания, $c$ - высота призмы.











