Понятие цилиндра
Геометрическая фигура, образованная двумя равными кругами, лежащими в параллельных плоскостях, все точки которых соединены между параллельными прямыми, так что никакая точка не остается несоединенной, называется цилиндром (рис. 1).
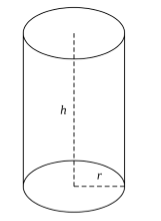
Рисунок 1. Цилиндр
Круги при этом называются основаниями цилиндра, а прямые их соединяющие -- образующими. Прямая, которая проходит через центры окружностей оснований называется осью цилиндра, а совокупность всех образующих -- боковой поверхностью цилиндра.
Виды цилиндров
Цилиндр, у которого все образующие перпендикулярны к плоскостям, проходящим через основания, называется прямым. В противном же случае он является наклонным (рис. 2).
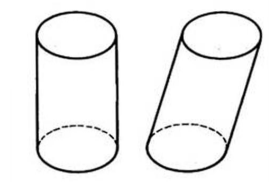
Рисунок 2. Прямой и наклонный цилиндры
Площадь поверхности цилиндра
Площадь поверхности цилиндра определяется следующим образом:
Найдем теперь формулы для вычисления площадь боковой поверхности и основания.
Так как в основании лежат круги, то очевидно, что
Площадь боковой поверхности цилиндра определяется как произведение длины окружности, ограничивающей основание цилиндра на его высоту.
Доказательство.
Для доказательства этой теоремы нам необходимо найти площадь развертки боковой поверхности цилиндра (рис. 3).
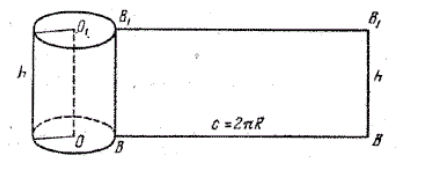
Рисунок 3.
Видим, что разверткой боковой поверхности цилиндра является прямоугольник. Высота прямоугольника равняется высоте цилиндра $h$, а длина равняется длине окружности, ограничивающей основание цилиндра, то есть
Теорема доказана.
Объем цилиндра
Объем цилиндра определяется как произведение площади основания цилиндра на его высоту.
Доказательство.
Рассмотрим цилиндр с радиусом $r$ и высотой $h$. Найдем ее объем $V$. Для этого сначала впишем в нее правильную $n-$угольную призму, в которую впишем еще один цилиндр. Пусть радиус второго цилиндра равняется $r'$, а её объем равен $V'$ (рис. 4).
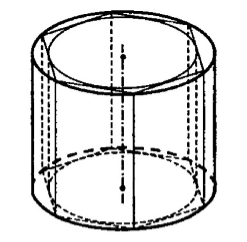
Рисунок 4.
Как мы знаем, объем призмы будет равен $S_{осн.пр.}h$. Следовательно, получим следующую оценку
Тогда из оценки, получим
Теорема доказана.
Пример задачи
Найти площадь полной поверхности цилиндра и его объем, если радиус его основания равняется $7$ см, а высота в два раза больше диаметра основания.
Решение.
Найдем вначале высоту цилиндра. Так как высота в два раза больше диаметра, получим
\[h=2\cdot 2r=4r=28\ см\]Как мы знаем
\[S_{осн}=\pi r^2=49\pi \]По теореме 1
\[S_{бок}=2\pi rh=392\pi \]Тогда
\[S_{полн}=S_{бок}+2S_{осн}=392\pi +98\pi =490\pi \]По теореме 2
\[V=\pi r^2h=49\pi \cdot 28=1372\pi \]Ответ: $490\pi ,\ 1372\pi $

















