Цилиндр, конус, шар

Цилиндр

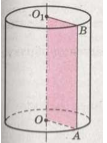
Рисунок 1.

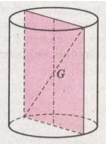
Рисунок 2.

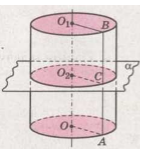
Рисунок 3.

Если прямоугольник $OABO$. вращается вокруг оси $001$ (рис. 1), его стороны $OA$ и $O_2B$ описывают равные круги, лежащие в параллельных плоскостях. Эти круги называют основаниями, а их радиус - радиусом цилиндра. Сторона $AB$, параллельная оси цилиндра, описывает кривую поверхность, которую называют боковой поверхностью цилиндра. Каждый отрезок этой поверхности, равный $AB$, - образующая цилиндра. Все образующие одного цилиндра равны и параллельны друг другу, поскольку каждая из них равна вращающейся стороне прямоугольника, и параллельна оси цилиндра. Длина образующей - высота цилиндра; она равна расстоянию между плоскостями оснований.

Все осевые сечения цилиндра - равные прямоугольники (рис. 2). Их диагонали проходят через середину $G$ отрезка, который соединяет центры оснований цилиндра. Поэтому точка $G$ - центр симметрии цилиндра. Плоскость, проходящая через точку $G$ перпендикулярно к оси цилиндра, - плоскость его симметрии. Другие плоскости симметрии цилиндра проходят через его ось.

Каждая секущая плоскость, перпендикулярная к оси цилиндра, пересекает его по кругу, равному основанию (рис. 3). Ведь любая точка $C$ образующей $AB$ отдалена от оси $OO_2$ на расстояние $CO_2 = OA$. Плоскость, пересекающая все образующие цилиндра, но не перпендикулярная к ним, пересекает боковую поверхность цилиндра по эллипсу (рис. 4).

Плоскость, которая проходит через образующую цилиндра и не имеет с ним других общих точек, называется касательной плоскостью к цилиндру. Она перпендикулярна к осевому сечению цилиндра, проведенному через эту же образующую (рис. 5).

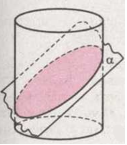
Рисунок 4.

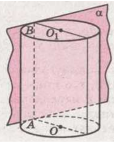
Рисунок 5.

Конус

Если прямоугольный треугольник $OPA$ вращать вокруг катета $PO$, его гипотенуза $PA$ опишет боковую поверхность, а катет $OA$ - круг - основание конуса (рис.6). Радиус этого круга называют радиусом конуса, точку $P$, отрезок $PO$, прямую $PO$ - соответственно вершиной, высотой и осью конуса. Все осевые сечения конуса - равные равнобедренные треугольники. Каждая плоскость, проходящая через ось конуса, является плоскостью его симметрии. Центра симметрии конус не имеет.

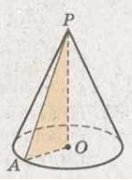
Рисунок 6.

Отрезок, соединяющий вершину конуса с любой точкой окружности его основания, - образующая конуса. Все образующие конуса равны, поскольку каждая из них равна гипотенузе треугольника, вращением которого образован конус. Плоскость, проходящая через образующую конуса и не имеющая с ним других общих точек, называется касательной плоскостью к конусу. Она перпендикулярна к осевому сечению, проведенному через эту же образующую (рис. 7).

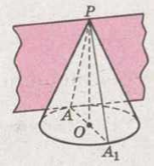
Рисунок 7.

Шар и сфера

Любой отрезок, соединяющий центр шара с какой-либо точкой его поверхности, называют радиусом шара. Длину этого отрезка также называют радиусом шара.

Отрезок, который соединяет две точки поверхности шара и проходит через центр, - диаметр шара, его концы - диаметрально противоположные точки шара.

Плоскость, которая проходит через диаметр шара, - диаметральная плоскость. Она является плоскостью симметрий шара и разбивает его на два равных полушара. Сечение шара диаметральной плоскостью называют большим кругом. Окружность больших кругов называют экватором шара, а точки пересечения поверхности шара с осью, перпендикулярной к плоскости экватора, - полюсами шара.

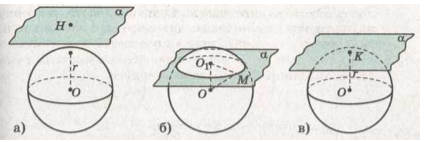
Рисунок 8.

Пусть расстояние от центра шара до плоскости равно $d$, а радиус шара $r$. Возможны три случая (рис. 8):

1. Если $d > r$, плоскость и шар не имеют общих точек (рис. 8а).

2. Если $d \[O_1M=\sqrt{r^2-d^2}.\]

   Из этой формулы следует, что сечение шара тем больше, чем меньше $d$, и что плоскости, равноудаленные от центра, пересекают шар по равных кругах.

3. Если $d = r$, плоскость и шар имеют только одну общую точку (рис. 8в). В этом случае говорят, что плоскость касается шара, а их общую точку называют точкой касания.