Понятие многогранника
Многогранником называется геометрическое тело в пространстве, которое ограниченно несколькими многоугольниками.
Примеры многогранников Вы можете видеть на рисунке 1.
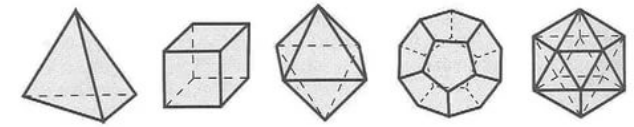
Рисунок 1. Примеры многогранников
При этом многоугольники, из которых состоят многогранники, называют гранями многогранника, стороны многоугольников -- сторонами многогранника, а вершины многоугольников -- вершинами многогранника.
Если многогранник всегда будет лежать по одну сторону от любой плоскости его граней, то многогранник называется выпуклым (рис. 2).
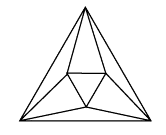
Рисунок 2. Выпуклый многогранник
Если многогранник лежит по разные стороны хотя бы одной плоскости его грани, то многогранник называется невыпуклым (рис. 3).
Рисунок 3. Невыпуклый многогранник
Рассмотрим далее детально, как пример многогранника, тетраэдр.
Тетраэдр
Понятие тетраэдра
Геометрическая фигура в пространстве, составленная из треугольника, вершины которого соединены с точкой, не лежащей в плоскости, содержащей треугольник, называется тетраэдром (рис. 4).
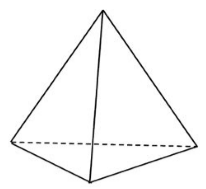
Рисунок 4. Тетраэдр
Таким образом, гранями тетраэдра являются $4$ треугольника.
Правильный тетраэдр
Тетраэдр, гранями которого являются четыре правильных треугольника, называется правильным тетраэдром.
Все боковые грани правильного тетраэдра и его основание являются равносторонними треугольниками, которые равны между собой.
Доказательство.
Рассмотрим правильный тетраэдр $ABCD$.
Так как все его грани правильные треугольники, то
Следовательно, по III признаку равенства треугольников все грани правильного тетраэдра равны между собой.
Теорема доказана.
Введем теперь следующее определение, связанное с понятием правильной пирамиды.
Апофемой правильного тетраэдра называется высота её боковой грани.
Очевидно, что по теореме один все апофемы равны между собой.
Площадь полной поверхности правильного тетраэдра определяется как удвоенное произведение длины основания на апофему.
Доказательство.
Обозначим сторону основания правильного тетраэдра через $a$, а апофему через $d$. Следовательно, площадь боковой грани равна
Так как, по теореме 1, все боковые стороны и основание равны, то
Теорема доказана.
Объем тетраэдра
Объем тетраэдра определяется трети произведения площади основания на высоту.
Доказательство.
Рассмотрим тетраэдр $ABCO$, с основанием $ABC$. Проведем высоту $OM_2$ и проведем через нее ось $Ox$ так, что точка $O$ - начало координат. Будем проводить сечения перпендикулярно оси $Ox$. Рассмотрим рисунок 5.
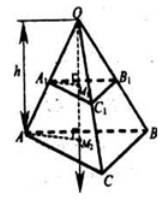
Рисунок 5.
Треугольники ${OA}_1B_1\ и\ OAB$, и треугольники ${OA}_1M_1\ и\ OAM$ подобны, значит
Аналогично
Значит, треугольники $A_1{B_1C}_1\ и\ ABC$ подобны с коэффициентом подобия $\frac{x}{h}$.
Значит
Следовательно
Теорема доказана.
Пример задачи
Найти площадь полной поверхности правильного тетраэдр, если её боковая сторона равняется $6$.
Решение.
Так как тетраэдр правильный, то по теореме Пифагора
\[d=\sqrt{6^2-3^2}=\sqrt{27}=3\sqrt{3}\]По теореме 2
\[S=2\cdot 6\cdot 3\sqrt{3}=36\sqrt{3}\]Ответ: $36\sqrt{3}\ $.












