Понятие конуса
Геометрическая фигура, образованная кругом и точкой, не лежащей в плоскости, содержащей этот круг, соединенной с каждой точкой окружности, ограничивающей этот круг, называется пирамидой (рис. 1).
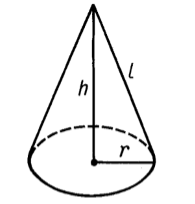
Рисунок 1. Конус
Круг, из которого составлен конус, называется основанием конуса, точка, не лежащая в плоскости основания -- вершиной конуса, прямые, соединяющие точку с основанием -- образующими конуса, а совокупность всех образующих -- боковой поверхностью конуса.
Площадь поверхности конуса
Площадь поверхности цилиндра определяется следующим образом:
Найдем теперь формулы для вычисления площадь боковой поверхности и основания.
Так как в основании лежит круг, то очевидно, что
Площадь боковой поверхности конуса определяется как половина произведения длины окружности, ограничивающей основание конуса на его образующую.
Доказательство.
Пусть нам дан конус с вершиной в точке $S$, радиусом основания, равным $R$ и образующей $l$. Для доказательства этой теоремы нам необходимо найти площадь развертки боковой поверхности цилиндра (рис. 2).
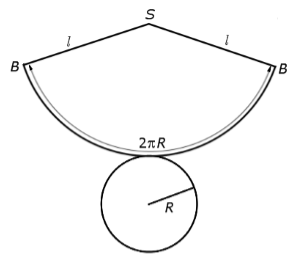
Рисунок 2.
Видим, что разверткой боковой поверхности цилиндра круговой сектор. Обозначим угол при вершине через $\alpha $. Как мы знаем, площадь кругового сектора равняется
Длина дуги кругового сектора равняется $2\pi R$, следовательно
Значит
Теорема доказана.
Усеченный конус
Если через обычный конус провести плоскость, параллельную её основанию, то фигура, образованная между этой плоскостью и плоскостью основания называется усеченным конусом (рис. 3).
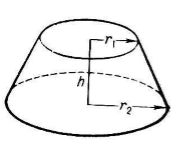
Рисунок 3. Усеченный конус
Площадь боковой поверхности усеченного конуса определяется как произведение полусуммы длин окружностей, ограничивающих основания на образующую.
Доказательство.
Обозначим радиусы оснований усеченного конуса через $r\ и\ r'$ соответственно, а апофему через $l$ (рис. 4).
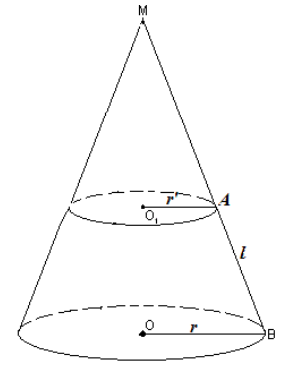
Рисунок 4.
Площадь боковой поверхности полного конуса по теореме 1
Площадь боковой поверхности отсеченного конуса по теореме 1
То есть
Из подобия прямоугольных треугольников, получим
То есть
Теорема доказана.
Пример задачи
Найти площадь полной поверхности конуса, если радиус его основания равняется $7$ см, образующая в два раза больше диаметра основания.
Решение.
Найдем вначале образующую. Так как образующая в два раза больше диаметра, получим
\[l=2\cdot 2r=4r=28\ см\]Как мы знаем
\[S_{осн}=\pi r^2=49\pi \]По теореме 1
\[S_{бок}=\pi rl=196\pi \]Тогда
\[S_{полн}=S_{бок}+S_{осн}=196\pi +49\pi =245\pi \]Ответ: $245\pi $












