Предварительные сведения
Перед тем как вводить свойства векторов, введем, непосредственно, понятие вектора, а также понятия их сложения, умножения на число и их равенства.
Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу - его концом. Направление указывается от его начала к концу отрезка.
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
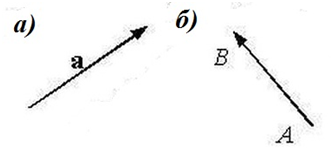
Обозначение: Двумя буквами: $\overline{AB}$ - (где $A$ его начало, а $B$ – его конец).
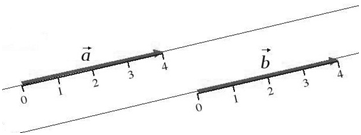
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Чтобы ввести определение равенства двух векторов, сначала нужно разобраться с такими понятиями, как коллинеарность, сонаправленность, противоположная направленность двух векторов, а также длину вектора.
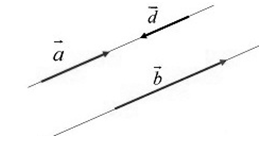
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
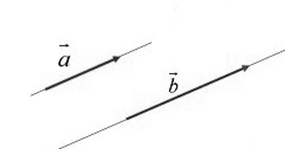
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $\overline{a}↑↑\overline{b}$
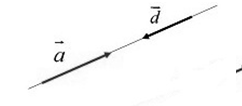
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $\overline{a}↑↓\overline{d}$
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Перейдем к определению равенства двух векторов
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Осталось ввести понятие сложения векторов, а также их умножения на число.
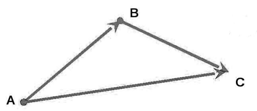
Суммой векторов $\overline{a+b}$ будем называть вектор $\overline{c}=\overline{AC}$, который построен следующим образом: От произвольной точки A отложем $\overline{AB}=\overline{a}$, далее от точки $B$ отложем $\overline{BC}=\overline{b}$ и соединим точку $A$ c точкой $C$ (рис. 6).
Произведением вектора $\overline{a}$ на $k∈R$ будем называть вектор $\overline{b}$ который будет удовлетворять условиям:
- $|\overline{b}|=|k||\overline{a}|$;
- $\overline{a}↑↑\overline{b}$ при $k≥0$ и, $\overline{a}↑↓\overline{b}$ при $k
Свойства сложения векторов
Введем свойства сложения для трех векторов $\overline{α}$, $\overline{β}$ и $\overline{γ}$:
-
Коммутативность сложения векторов:
$\overline{α}+\overline{β}=\overline{β}+\overline{α}$
-
Ассоциативность трех векторов по сложению:
$(\overline{α}+\overline{β})+\overline{γ}=\overline{α}+(\overline{β}+\overline{γ})$
-
Сложение с нулевым вектором:
$\overline{α}+\overline{0}=\overline{α}$
-
Сложение противоположных векторов
$\overline{α}+(\overline{-α})=\overline{0}$
Все эти свойства можно легко проверить с помощью построений таких векторов с помощью определения 8. В двух первых сравнением построенных векторов с правой и левой частей равенства, а в третьем и четвертом с помощью построения вектора с левой стороны.
Свойства умножения вектора на число
Введем свойства умножения для двух векторов $\overline{α}$, $\overline{β}$ и чисел $a$ и $b$.
- $a(\overline{α}+\overline{β})=a\overline{α}+a\overline{β}$
- $\overline{α}(a+b)=\overline{α}a+\overline{α}b$
- $(ab)\overline{α}=a(b\overline{α})=b(a\overline{α})$
- $1\cdot \overline{α}=\overline{α}$
Все эти свойства можно легко проверить с использованием определений 8 и 9. В двух первых сравнением построенных векторов с правой и левой частей равенства, в третьем сравнением всех векторов, входящих в равенство, и в четвертом с помощью построения вектора с левой стороны.
Пример задачи
Провести сложение векторов
$2\overline{AB}+(2\overline{BC}+3\overline{AC})$
Решение.
Используя свойство сложения 2, получим:
$2\overline{AB}+(2\overline{BC}+3\overline{AC})=(2\overline{AB}+2\overline{BC})+3\overline{AC}$
Используя свойство умножения на число 1, получим:
$(2\overline{AB}+2\overline{BC})+3\overline{AC}=2(\overline{AB}+\overline{BC})+3\overline{AC}=2\overline{BC}+3\overline{AC}=5\overline{AC}$
Ответ: $5\overline{AC}$.