Откладывание вектора от данной точки
Для того, чтобы ввести сумму векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.
Если точка $A$ начала какого-либо вектора $\overrightarrow{a}$, то говорят, что вектор $\overrightarrow{a}$ отложен от точки $A$ (рис. 1).
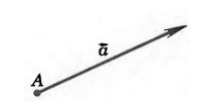
Рисунок 1. $\overrightarrow{a}$ отложенный от точки $A$
Введем следующую теорему:
От любой точки $K$ можно отложить вектор $\overrightarrow{a}$ и притом только один.
Доказательство.
Существование: Здесь нужно рассмотреть два случая:
-
Вектор $\overrightarrow{a}$ - нулевой.
В этом случае, очевидно, что искомый вектор -- вектор $\overrightarrow{KK}$.
-
Вектор $\overrightarrow{a}$ - ненулевой.
Обозначим точкой $A$ начало вектора $\overrightarrow{a}$, а точкой $B$ - конец вектора $\overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $\overrightarrow{a}$. Отложим на этой прямой отрезки $\left|KL\right|=|AB|$ и $\left|KM\right|=|AB|$. Рассмотрим векторы $\overrightarrow{KL}$ и $\overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $\overrightarrow{a}$ (рис. 2)
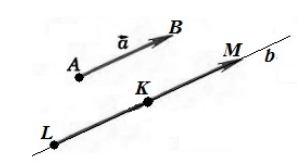
Рисунок 2. Иллюстрация теоремы 1
Единственность: единственность сразу следует из построения, проведенного в пункте «существование».
Теорема доказана.
Сложение векторов. Правило треугольника
Пусть нам даны векторы $\overrightarrow{a}$ и $\overrightarrow{b}$.
Суммой векторов $\overrightarrow{a}+\overrightarrow{b}$ называется вектор $\overrightarrow{c}=\overrightarrow{AC}$, построенный следующим образом: От произвольной точки $A$ отклабывается вектор $\overrightarrow{AB}=\overrightarrow{a}$, затем от полученной точки $B$ откладывается вектор $\overrightarrow{BC}=\overrightarrow{b}$ и соединяют точку $A$ c точкой $C$ (рис. 3).
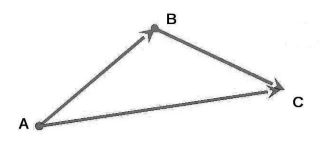
Рисунок 3. Сумма векторов
Иначе, определение 2, еще называют правилом треугольника для сложения двух векторов.
Из этого правила следует несколько свойств сложения двух векторов:
-
Для любого вектора $\overrightarrow{a}$ выполняется равенство
\[\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{a}\] -
Для любых произвольных точек $A,\ B\ и\ C$ выполняется равенство
\[\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\]
Аналогично правилу треугольника можно строить сумму любого количества векторов. Такое правило сложения называется правилом многоугольника.
Правило параллелограмма
Помимо правила треугольника для сложения двух векторов, есть еще правило параллелограмма для сложения двух векторов. Сформулируем и докажем для начала следующую теорему.
Для любых треух векторов $\overrightarrow{a},\ \overrightarrow{b}\ и\ \overrightarrow{c}$ справедливы следующие два закона:
- Переместительный закон:
- Сочетательный закон:
Доказательство.
Переместительный закон:
-
Пусть векторы $\overrightarrow{a}\ и\ \overrightarrow{b}$ не коллинеарны.
Возьмем произвольную точку $A$ и построим от нее (на одном рисунке) суммы $\overrightarrow{a}+\overrightarrow{b}\ и\ \overrightarrow{b}+\overrightarrow{a}$. Получим следующий рисунок (рис 4).
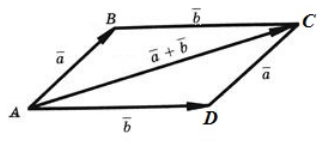
Рисунок 4. Иллюстрация переместительного законаОчевидно, что $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, а $\overrightarrow{b}+\overrightarrow{a}=\overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AC}$
Следовательно, $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}$.
-
Пусть векторы $\overrightarrow{a}\ и\ \overrightarrow{b}$ коллинеарны.
Тогда выполнение переместительно закона будет очевидно вытекать из равенства длин $\left|\overrightarrow{a}+\overrightarrow{b}\right|и\ |\overrightarrow{b}+\overrightarrow{a}|$.
Сочетательный закон:
Построим следующий рисунок: Отложим от произвольной точки $A$ вектор $\overrightarrow{AB}=\overrightarrow{a}$, от полученной точки $B$ -- вектор $\overrightarrow{BC}=\overrightarrow{b}$ и от точки $C$ -- вектор $\overrightarrow{CD}=\overrightarrow{c}$ (Рис. 5).
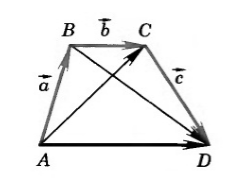
Рисунок 5. Иллюстрация сочетательного закона
Из свойства правила треугольника $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, получим:
Следовательно, $\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}=\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)$.
Теорема доказана.
Из этой теоремы мы теперь можем выделить правило параллелограмма для суммы двух неколлинеарных векторов: чтобы сложить два неколлинеарных вектора $\overrightarrow{a}$ и $\overrightarrow{b}$, нужно отложить от произвольной точки $A$ векторы $\overrightarrow{AB}=\overrightarrow{a}$ и $\overrightarrow{AD}=\overrightarrow{b}$ и построить параллелограмм $ABCD$. Тогда $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AC}$.
Пример задачи на сложение векторов
Дан четырехугольник $ABCD$. Доказать, что $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AD}$
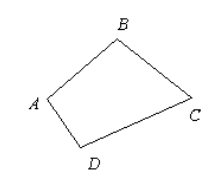
Рисунок 6.
Доказательство.
Воспользуемся свойством правила треугольника $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, получим:
\[\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}\]ч. т. д.












