Правило параллелепипеда
Для правила сложения трех векторов рассмотрим следующую задачу.
Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_1}=\overrightarrow{AC_1}$
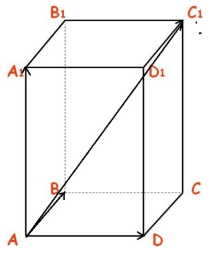
Рисунок 1.
Доказательство.
Воспользуемся свойством правила треугольника сложения двух векторов $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, получим:
\[\overrightarrow{AC_1}=\overrightarrow{AC}+\overrightarrow{CC_1}=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{CC_1}\]Так как $\overrightarrow{DC}=\overrightarrow{AB},\ \ \overrightarrow{CC_1}=\overrightarrow{AA_1}$
То есть
\[\overrightarrow{AC_1}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_1}\]ч. т. д.
Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $\overrightarrow{a},\overrightarrow{b}\ и\ \overrightarrow{c}$ нужно от произвольной точки $O$ отложить векторы $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{AC}=\overrightarrow{b}$ и $\overrightarrow{AA_1}=\overrightarrow{c}$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $\overrightarrow{AC_1}$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.
Разложение вектора по двум неколлинеарным векторам
Вспомним сначала, какие векторы называются компланарными.
Два вектора, которые параллельны одной плоскости называются компланарными.
Произвольный вектор $\overrightarrow{p}$ можно разложить по трем некомпланарным векторам $\overrightarrow{a_1},\ \overrightarrow{a_2}$ и $\overrightarrow{a_3}$ с единственными коэффициентами разложения.
Математически это можно записать следующим образом
\[\overrightarrow{p}={\alpha }_1\overrightarrow{a_1}+{\alpha }_2\overrightarrow{a_2}+{\alpha }_3\overrightarrow{a_3}\]Доказательство.
Существование: Пусть нам даны три некомпланарных вектора $\overrightarrow{a_1},\ \overrightarrow{a_2}$ и $\overrightarrow{a_3}$. Выберем произвольную точку $O$ и построим следующие векторы:
\[\overrightarrow{a_1}=\overrightarrow{OA},\ \overrightarrow{a_2}=\overrightarrow{OB},\ \overrightarrow{a_3}=\overrightarrow{OC}\ и\ \overrightarrow{p}=\overrightarrow{OP}\]Рассмотрим следующий рисунок:
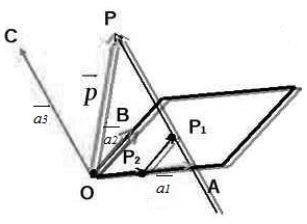
Рисунок 2.
Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $\overrightarrow{OC}$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $\overrightarrow{OB}$. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).
Воспользуемся свойством правила треугольника сложения двух векторов $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, получим:
\[\overrightarrow{OP}=\overrightarrow{p}=\overrightarrow{OP_2}+\overrightarrow{P_2P_1}+\overrightarrow{P_1P}\]Так как векторы $\overrightarrow{OP_2}$ и $\overrightarrow{OA}$ коллинеарны, то
\[\overrightarrow{OP_2}={\alpha }_1\overrightarrow{OA}={\alpha }_1\overrightarrow{a_1}\]Так как векторы $\overrightarrow{P_2P_1}$ и $\overrightarrow{OB}$ коллинеарны, то
\[\overrightarrow{P_2P_1}={\alpha }_2\overrightarrow{OB}={\alpha }_2\overrightarrow{a_2}\]Так как векторы $\overrightarrow{P_1P}$ и $\overrightarrow{OC}$ коллинеарны, то
\[\overrightarrow{P_1P}={\alpha }_3\overrightarrow{OC}={\alpha }_3\overrightarrow{a_3}\]Тогда, получаем, что
\[\overrightarrow{p}=\overrightarrow{OP_2}+\overrightarrow{P_2P_1}+\overrightarrow{P_1P}={\alpha }_1\overrightarrow{a_1}+{\alpha }_2\overrightarrow{a_2}+{\alpha }_3\overrightarrow{a_3}\]Существование разложения доказано.
Единственность: Предположим противное. Пусть существует еще одно разложение вектора $\overrightarrow{p}$ по векторам $\overrightarrow{a_1},\ \overrightarrow{a_2}$ и $\overrightarrow{a_3}$:
\[\overrightarrow{p}={\alpha '}_1\overrightarrow{a_1}+{\alpha '}_2\overrightarrow{a_2}+{\alpha '}_3\overrightarrow{a_3}\]Вычтем эти разложения друг из друга
\[\overrightarrow{p}-\overrightarrow{p}={\alpha }_1\overrightarrow{a_1}+{\alpha }_2\overrightarrow{a_2}+{\alpha }_3\overrightarrow{a_3}-{\alpha '}_1\overrightarrow{a_1}-{\alpha '}_2\overrightarrow{a_2}-{\alpha '}_3\overrightarrow{a_3}\] \[\overrightarrow{0}=\left({\alpha }_1-{{\alpha }'}_1\right)\overrightarrow{a_1}+\left({\alpha }_2-{{\alpha }'}_2\right)\overrightarrow{a_2}+({\alpha }_3-{{\alpha }'}_3)\overrightarrow{a_3}\]Из этого получаем
\[\left\{ \begin{array}{c} {{\alpha }_1-{{\alpha }'}_1=0,} \\ {{\alpha }_2-{{\alpha }'}_2=0} \\ {{\alpha }_3-{{\alpha }'}_3=0.} \end{array} \right.\]Следовательно
\[\left\{ \begin{array}{c} {{\alpha }_1={{\alpha }'}_1,} \\ {{\alpha }_2={{\alpha }'}_2,} \\ {{\alpha }_3={{\alpha }'}_3.} \end{array} \right.\]Теорема доказана.
Пример задачи
Пусть нам дана пирамида $OABCD$. Разложите вектор $\overrightarrow{OD}$ по векторам $\overrightarrow{OA},\ \overrightarrow{OB}\ и\ \overrightarrow{OC}$.
Решение.
Так как векторы $\overrightarrow{OA},\ \overrightarrow{OB}\ и\ \overrightarrow{OC}$ - стороны пирамиды, то они являются некомпланарными векторами. Тогда, по теореме 1, вектор $\overrightarrow{OD}$ можно разложить по этим векторам, причем разложение будет единственно. Для разложения будем пользоваться свойством сложения векторов и равенством векторов.
Видим, что
\[\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{AD}\] \[\overrightarrow{AD}=\overrightarrow{BC}=\overrightarrow{BO}+\overrightarrow{OC}=\overrightarrow{OC}-\overrightarrow{OB}\]Следовательно
\[\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}\]Ответ: $\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}.$

















