Откладывание вектора от данной точки
Для того, чтобы ввести разность векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.
Если точка $A$ начала какого-либо вектора $\overrightarrow{a}$, то говорят, что вектор $\overrightarrow{a}$ отложен от точки $A$ (рис. 1).
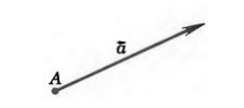
Рисунок 1. $\overrightarrow{a}$ отложенный от точки $A$
Введем следующую теорему:
От любой точки $K$ можно отложить вектор $\overrightarrow{a}$ и притом только один.
Доказательство.
Существование: Здесь нужно рассмотреть два случая:
-
Вектор $\overrightarrow{a}$ - нулевой.
В этом случае, очевидно, что искомый вектор -- вектор $\overrightarrow{KK}$.
-
Вектор $\overrightarrow{a}$ -- ненулевой.
Обозначим точкой $A$ -- начало вектора $\overrightarrow{a}$, а точкой $B$ - конец вектора $\overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $\overrightarrow{a}$. Отложим на этой прямой отрезки $\left|KL\right|=|AB|$ и $\left|KM\right|=|AB|$. Рассмотрим векторы $\overrightarrow{KL}$ и $\overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $\overrightarrow{a}$ (рис. 2)
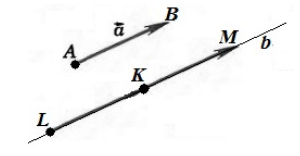
Рисунок 2. Иллюстрация теоремы 1
Единственность: единственность сразу следует из построения, проведенного в пункте «существование».
Теорема доказана.
Вычитание векторов. Правило первое
Пусть нам даны векторы $\overrightarrow{a}$ и $\overrightarrow{b}$.
Разностью двух векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ называется такой вектор $\overrightarrow{c}$, который при сложении с вектором $\overrightarrow{b}$ дает вектор $\overrightarrow{a}$, то есть
\[\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{a}\]Обозначение: $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{c}$.
Построение разности двух векторов рассмотрим с помощью задачи.
Пусть даны векторы $\overrightarrow{a}$ и $\overrightarrow{b}$. Построить вектор $\overrightarrow{a}-\overrightarrow{b}$.
Решение.
Построим произвольную точку $O$ и отложим от нее векторы $\overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OB}=\overrightarrow{b}$. Соединив точку $B$ с точкой $A$, получим вектор $\overrightarrow{BA}$ (рис. 3).
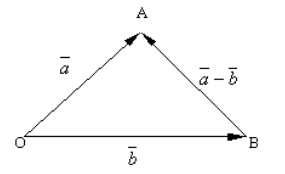
Рисунок 3. Разность двух векторов
По правилу треугольника для построения суммы двух векторов видим, что
\[\overrightarrow{OB}+\overrightarrow{BA}=\overrightarrow{OA}\]То есть
\[\overrightarrow{b}+\overrightarrow{BA}=\overrightarrow{a}\]Из определения 2, получаем, что
\[\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{BA}\]Ответ: $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{BA}$.
Из этой задачи получаем следующее правило для нахождения разности двух векторов. Чтобы найти разность $\overrightarrow{a}-\overrightarrow{b}$ нужно от произвольной точки $O$ отложить векторы $\overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OB}=\overrightarrow{b}$ и соединить конец второго вектор с концом первого вектора.
Вычитание векторов. Правило второе
Вспомним следующее необходимое нам понятие.
Вектор $\overrightarrow{a_1}$ называется произвольным для вектора $\overrightarrow{a}$, если эти векторы противоположно направлены и имеют равную длину.
Обозначение: Вектор $(-\overrightarrow{a})$ противоположный для вектора $\overrightarrow{a}$.
Для того чтобы ввести второе правило для разности двух векторов, нам необходимо в начале ввести и доказать следующую теорему.
Для любых двух векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ справедливо следующее равенство:
\[\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})\]Доказательство.
По определению 2, имеем
Прибавим к обеим частям вектор $\left(-\overrightarrow{b}\right)$, получим
Так как векторы $\overrightarrow{b}$ и $\left(-\overrightarrow{b}\right)$ противоположны, то $\overrightarrow{b}+\left(-\overrightarrow{b}\right)=\overrightarrow{0}$. Имеем
Теорема доказана.
Из этой теоремы получаем следующее правило для разности двух векторов: Чтобы найти разность $\overrightarrow{a}-\overrightarrow{b}$ нужно от произвольной точки $O$ отложить вектор $\overrightarrow{OA}=\overrightarrow{a}$, затем от полученной точки $A$ отложить вектор $\overrightarrow{AB}=-\overrightarrow{b}$ и соединить начало первого вектора с концом второго вектора.
Пример задачи на понятие разности векторов
Пусть дан параллелограмм $ADCD$, диагонали которого пересекаются в точке $O$. $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{AD}=\overrightarrow{b}$ (рис. 4). Выразить через векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ следующие векторы:
а) $\overrightarrow{DC}+\overrightarrow{CB}$
б) $\overrightarrow{BO}-\overrightarrow{OC}$
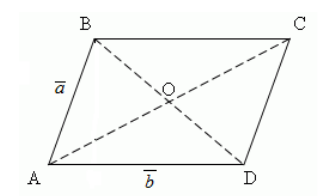
Рисунок 4. Параллелограмм
Решение.
а) Произведем сложение по правилу треугольника, получим
\[\overrightarrow{DC}+\overrightarrow{CB}=\overrightarrow{DB}\]Из первого правила разности двух векторов, получаем
\[\overrightarrow{DB}=\overrightarrow{a}-\overrightarrow{b}\]б) Так как $\overrightarrow{OC}=\overrightarrow{AO}$, получим
\[\overrightarrow{BO}-\overrightarrow{OC}=\overrightarrow{BO}-\overrightarrow{AO}\]По теореме 2, имеем
\[\overrightarrow{BO}-\overrightarrow{AO}=\overrightarrow{BO}+\left(-\overrightarrow{AO}\right)=\overrightarrow{BO}+\overrightarrow{OA}\]Используя правило треугольника, окончательно имеем
\[\overrightarrow{BO}+\overrightarrow{OA}=\overrightarrow{BA}=-\overrightarrow{AB}=-\overrightarrow{a}\]

















