Сущность векторного метода для решения геометрических задач
Векторный метод решения задач основан на решении задач с использованием аппарата векторной алгебры.
Применение векторной алгебры к решению геометрических задач основано на следующих основных утверждениях.
Утверждение 1 (Необходимое и достаточное условие коллинеарности векторов): Два ненулевых вектора →a и →b коллинеарны тогда и только тогда, когда существует действительное число k≠0, такое, что удовлетворяется следующее равенство
Утверждение 2: Если векторы →a и →b не коллинеарны, то любой вектор →c, компланарный с данными векторами можно представить в виде линейной комбинации и притом единственным образом:
Утверждение 3: Любой вектор →d в трехмерном пространстве можно разложить по трем некомпланарным векторам →a, →b и →c:
При решении задач векторным методом также применяются такие понятия, как сложение, вычитание векторов, умножение вектора на число, а также понятие скалярного произведения векторов.
Общая схема для решения геометрических задач векторным методом
При решении геометрических задач векторным методом рекомендуется пользоваться следующей схемой:
-
Провести анализ условия задачи:
а) Выяснить в какой системе координат (двумерной или трехмерной) рассматривается данная задача;
б) Записать, что нам дано, что нужно найти или доказать, а также построить чертеж по условию задачи.
-
Перевести условие задачи и требования к векторному виду.
-
Составить векторные соотношения, соответствующие тому, что дано в задаче и привести их к векторным соотношениям, соответствующим требованиям задачи.
-
Перевести полученный результат на геометрический язык.
Примеры типов задач, которые решаются векторным методом
Приведем теперь примеры классических задач, решаемых с помощью векторного метода (Не приводя их решений).
-
Задачи на доказательство параллельности.
-
Задачи на нахождение отношений, в котором точка делит отрезок.
-
Задачи на доказательство принадлежности трех точек одной прямой.
-
Задачи на доказательство принадлежности четырех точек одной плоскости.
-
Задачи на доказательство перпендикулярности.
-
Задачи на вычисление длины отрезка.
-
Задачи на нахождение величины угла.
-
Задачи на вычисление площадей и объемов геометрических фигур.
Примеры задач на применение векторного метода
Далее рассмотрим ряд задач, которые решаются с помощью векторного метода.
Доказать, что линия, соединяющая середины диагоналей произвольной трапеции параллельна основаниям этой трапеции и равна их полуразности.
Доказательство.
Пусть нам дана трапеция ABCD. MN - отрезок, соединяющий середины диагоналей данной трапеции (рис. 1).
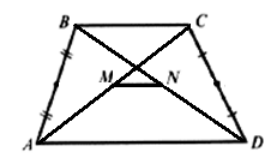
Рисунок 1.
Докажем, что MN=AD−BC2 и MN||AD
Рассмотрим вектор →MN. Используя правило многоугольника для сложения векторов, с одной стороны, получим
→MN=→MA+→AD+→DNС другой стороны
→MN=→MC+→CB+→BNСложим два последних равенства:
2→MN=→MA+→AD+→DN+→MC+→CB+→BNТак как MN - отрезок, соединяющий середины диагоналей, то
→MA+→MC=→0, →DN+→BN=→0Тогда получим
2→MN=→AD+→CB=→AD−→BCТо есть
→MN=→AD−→BC2Так как →AD и →BC сонаправлены, то →MN||→AD.
Из этого получаем, что MN=AD−BC2 и MN||AD
ч. т. д.
На сторонах треугольника ABC взяты точки L, M, K, так что |BL|=3|AL|, |BM|=2|CM|, |AK|=2|CK|. Найти, в каком отношении прямая KL делит отрезок AM.
Решение.
Обозначим через точку E - точку пересечения отрезка AM с прямой KL(рис. 2).
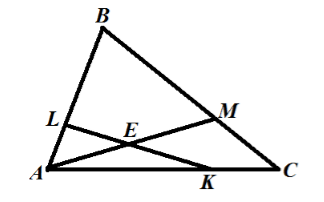
Рисунок 2.
Найдем |AE|:|EM|
Введем, для удобства, следующие обозначения: →AB=→b, →AC=→c, →AE=x→AM, →LE=y→LK
Воспользуемся далее правилом треугольника для сложения векторов. С одной стороны получим
→AE=x→AM=x(→AB+→BM)=x(→b+23(→c−→b))=23x→c−13x→bС другой стороны
→AE=→AL+→LE=→AL+y→LK=14→b+y(23→c−14→b)=23y→c+14→b−14y→bТогда
23x→c−13x→b=23y→c+14→b−14y→bПолучаем систему:
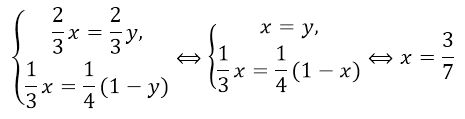
Рисунок 3.
→AE=37→AM, следовательно
Ответ: 3:4.
