Откладывание вектора от данной точки
Перед тем как ввести понятие суммы, разности векторов и умножения вектора на число, вначале разберем такое понятие, как откладывание вектора от точки.
Если точка $A$ начала какого-либо вектора $\overrightarrow{a}$, то говорят, что вектор $\overrightarrow{a}$ отложен от точки $A$ (рис. 1).
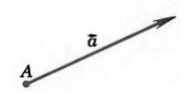
Рисунок 1.
От любой точки $K$ можно отложить вектор единственный $\overrightarrow{a}$.
Доказательство.
Существование: Имеем два следующих случая:
-
Вектор $\overrightarrow{a}$ - нулевой.
Здесь получаем, что искомый нами вектор совпадает с вектором $\overrightarrow{KK}$.
-
Вектор $\overrightarrow{a}$ не является нулевым.
Пусть точка $A$ является началом вектора $\overrightarrow{a}$, а точкой $B$ - конец вектора $\overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $\overrightarrow{a}$. Будем откладывать на прямой отрезки $\left|KL\right|=|AB|$ и $\left|KM\right|=|AB|$. Рассмотрим векторы $\overrightarrow{KL}$ и $\overrightarrow{KM}$. Из этих двух векторов нужный нам вектор -- вектор, сонаправленный с вектором $\overrightarrow{a}$ (рис.2)
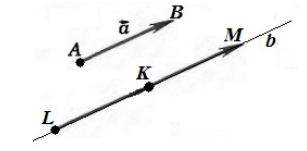
Рисунок 2.
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сложение векторов. Правило треугольника
Рассмотрим векторы $\overrightarrow{a}$ и $\overrightarrow{b}$.
Вектор $\overrightarrow{c}=\overrightarrow{AC}$ называется суммой векторов $\overrightarrow{a}+\overrightarrow{b}$ который получается из векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ следующим образом: От точки $A$ отложим $\overrightarrow{AB}=\overrightarrow{a}$, от точки $B$ отложим $\overrightarrow{BC}=\overrightarrow{b}$ и соединим точку $A$ c точкой $C$ (рис. 3).
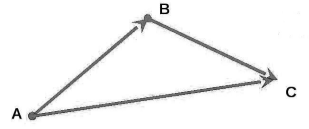
Рисунок 3.
Также это определение называется правилом треугольника для сложения двух векторов.
Отметим несколько свойств сложения двух векторов:
-
Для произвольного вектора $\overrightarrow{a}$ выполняется равенство
\[\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{a}\] -
Для произвольных точек $A,\ B\ и\ C$ справедливо следующее равенство
\[\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\]
Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Вычитание векторов
Рассмотрим векторы $\overrightarrow{a}$ и $\overrightarrow{b}$.
Разностью двух векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ называется такой вектор $\overrightarrow{c}$, который при сложении с вектором $\overrightarrow{b}$ дает вектор $\overrightarrow{a}$, то есть
\[\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{a}\]Обозначение: $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{c}$.
Построение разности двух векторов рассмотрим с помощью задачи
Пусть даны векторы $\overrightarrow{a}$ и $\overrightarrow{b}$. Построить вектор $\overrightarrow{a}-\overrightarrow{b}$.
Решение.
Построим произвольную точку $O$ и отложим от нее векторы $\overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OB}=\overrightarrow{b}$. Соединив точку $B$ с точкой $A$, получим вектор $\overrightarrow{BA}$ (рис. 4).
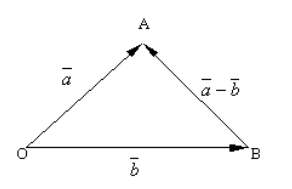
Рисунок 4.
По правилу треугольника для построения суммы двух векторов видим, что
\[\overrightarrow{OB}+\overrightarrow{BA}=\overrightarrow{OA}\]То есть
\[\overrightarrow{b}+\overrightarrow{BA}=\overrightarrow{a}\]Из определения 2, получаем, что
\[\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{BA}\]Ответ: $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{BA}$.
Из этой задачи получаем следующее правило для нахождения разности двух векторов. Чтобы найти разность $\overrightarrow{a}-\overrightarrow{b}$ нужно от произвольной точки $O$ отложить векторы $\overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OB}=\overrightarrow{b}$ и соединить конец второго вектор с концом первого вектора.
Умножение вектора на число
Пусть нам дан вектор $\overrightarrow{a\ }$ и действительное число $k$.
Произведением вектора $\overrightarrow{a\ }$ на действительное число $k$ называется вектор $\overrightarrow{b\ }$ удовлетворяющий следующим условиям:
-
Длина вектора $\overrightarrow{b\ }$ равна $\left|\overrightarrow{b\ }\right|=\left|k\right||\overrightarrow{a\ }|$;
Векторы $\overrightarrow{a\ }$ и $\overrightarrow{b\ }$ сонаправлены, при $k\ge 0$ и противоположно направлены, если $k
Обозначение: $\ \overrightarrow{b\ }=k\overrightarrow{a\ }$.
Пример задачи
Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_1}=\overrightarrow{AC_1}$
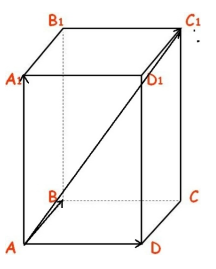
Рисунок 5.
Доказательство.
Воспользуемся свойством правила треугольника $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, получим:
\[\overrightarrow{AC_1}=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{CC_1}\]Так как $\overrightarrow{DC}=\overrightarrow{AB},\ \ \overrightarrow{CC_1}=\overrightarrow{AA_1}$
То есть
\[\overrightarrow{AC_1}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_1}\]ч. т. д.














