Как найти скалярное произведение векторов

Угол между векторами

Рассмотрим два данных вектора $\overrightarrow{a}$ и $\overrightarrow{b}$. Отложим от произвольно выбранной точки $O$ векторы $\overrightarrow{a}=\overrightarrow{OA}$ и $\overrightarrow{b}=\overrightarrow{OB}$, тогда угол $AOB$ называется углом между векторами $\overrightarrow{a}$ и $\overrightarrow{b}$ (рис. 1).

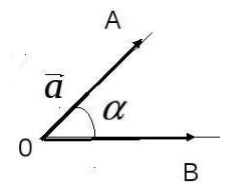
Рисунок 1.

Отметим здесь, что если векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ сонаправлены или один из них является нулевым вектором, тогда угол между векторами равен $0^0$.

Обозначение: $\widehat{\overrightarrow{a},\overrightarrow{b}}$

Понятие скалярного произведения векторов

Математически это определение можно записать следующим образом:

Скалярное произведение может равняться нулю в двух случаях:

1. Если один из векторов будет нулевым вектором (Так как тогда его длина равна нулю).

2. Если векторы будут взаимно перпендикулярны (то есть $cos{90}^0=0$).

Отметим также, что скалярное произведение больше нуля, если угол между этими векторами острый (так как ${cos \left(\widehat{\overrightarrow{a},\overrightarrow{b}}\right)\ } >0$), и меньше нуля, если угол между этими векторами тупой (так как ${cos \left(\widehat{\overrightarrow{a},\overrightarrow{b}}\right)\ }

С понятием скалярного произведения связано понятие скалярного квадрата.

Вычисление скалярного произведения по координатам векторов

Помимо стандартного способа нахождения значения скалярного произведения, который вытекает из определения, существует еще один способ.

Рассмотрим его.

Пусть векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ имеют координаты $\left(a_1,b_1\right)$ и $\left(a_2,b_2\right)$, соответственно.

Доказательство.

1. Пусть один из векторов будет нулевым вектором. К примеру, $\overrightarrow{a}=(0,0)$.

   Тогда $\overrightarrow{a}\overrightarrow{b}=0$. С другой стороны $a_1a_2+b_1b_2=0\cdot a_2+0\cdot b_2=0$, значит

   \[\overrightarrow{a}\overrightarrow{b}=a_1a_2+b_1b_2\]

2. Оба вектора не будут нулевыми векторами.

   Отложим от произвольной точки $O$ векторы $\overrightarrow{OA}$ и $\overrightarrow{OB}$ (рис. 2).

   
   
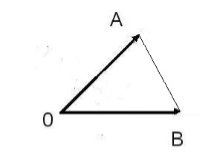
   Рисунок 2. Иллюстрация теоремы 1

   По теореме косинусов, получим:

   \[{AB}^2={OA}^2+{OB}^2-2OA\cdot OBcosO\]

   Так как $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$, получим

   \[{|\overrightarrow{OB}-\overrightarrow{OA}|}^2={|\overrightarrow{OA}|}^2+{|\overrightarrow{OB}|}^2-2\left|\overrightarrow{OA}\right||\overrightarrow{OB}|\] \[\overrightarrow{OA}\overrightarrow{OB}=\frac{1}{2}\left({|\overrightarrow{OA}|}^2+{|\overrightarrow{OB}|}^2-{|\overrightarrow{OB}-\overrightarrow{OA}|}^2\right)\]

   Так как векторы $\overrightarrow{OA}$ и $\overrightarrow{OB}$ имеют координаты $\left(a_1,b_1\right)$ и $\left(a_2,b_2\right)$, соответственно, то $\overrightarrow{OB}-\overrightarrow{OA}=\left(a_2-a_1,b_2-b_1\right)$. Тогда равенство примет вид

   \[\overrightarrow{OA}\overrightarrow{OB}=\frac{1}{2}\left(a^2_1+b^2_1+a^2_2+b^2_2-{(a_2-a_1)}^2-{(b_2-b_1)}^2\right)=a_1a_2+b_1b_2\]

Теорема доказана.

Эта теорема имеет несколько следствий:

Следствие 1: Векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ перпендикулярны тогда и только тогда, когда $a_1a_2+b_1b_2=0$

Следствие 2: Косинус угла между векторами равен $cos\alpha =\frac{a_1a_2+b_1b_2}{\sqrt{a^2_1+b^2_1}\cdot \sqrt{a^2_2+b^2_2}}$

Свойства скалярного произведения векторов

Для любых трех векторов и действительного числа $k$ справедливо:

1. ${\overrightarrow{a}}^2\ge 0$

   Данное свойство следует из определения скалярного квадрата (определение 2).

2. Переместительный закон: $\overrightarrow{a}\overrightarrow{b}=\overrightarrow{b}\overrightarrow{a}$.

   Данное свойство следует из определения скалярного произведения (определение 1).

3. Распределительный закон:

   $\left(\overrightarrow{a}+\overrightarrow{b}\right)\overrightarrow{c}=\overrightarrow{a}\overrightarrow{c}+\overrightarrow{b}\overrightarrow{c}$. \end{enumerate}

   По теореме 1, имеем:

   \[\left(\overrightarrow{a}+\overrightarrow{b}\right)\overrightarrow{c}=\left(a_1+a_2\right)a_3+\left(b_1+b_2\right)b_3=a_1a_3+a_2a_3+b_1b_3+b_2b_3==\overrightarrow{a}\overrightarrow{c}+\overrightarrow{b}\overrightarrow{c}\]

4. Сочетательный закон: $\left(k\overrightarrow{a}\right)\overrightarrow{b}=k(\overrightarrow{a}\overrightarrow{b})$. \end{enumerate}

   По теореме 1, имеем:

   \[\left(k\overrightarrow{a}\right)\overrightarrow{b}=ka_1a_2+kb_1b_2=k\left(a_1a_2+b_1b_2\right)=k(\overrightarrow{a}\overrightarrow{b})\]

Пример задачи на вычисление скалярного произведения векторов