Угол между векторами
Для того, чтобы мы могли ввести формулу для вычисления угла между векторами через координаты, нужно сначала разобраться с самим понятием угла между этими векторами.
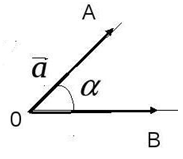
Пусть нам даны два вектора $\overline{α}$ и $\overline{β}$. Возьмем в пространстве какую-либо точку $O$ и отложим от нее векторы $\overline{α}=\overline{OA}$ и $\overline{β}=\overline{OB}$, тогда угол $AOB$ будет носить название угол между двумя векторами. (рис. 1).
Рисунок 1. Угол между векторами. Автор24 — интернет-биржа студенческих работ
Причем мы будем считать, что если векторы $\overline{α}$ и $\overline{β}$ будут сонаправленными, или один или оба из них будет нулевым вектором, то угол между этими векторами будет равняться $0^\circ$.
Обозначение: $∠(\overline{α},\overline{β})$
Нахождение угла между векторами в пространстве с помощью скалярного произведения
Вспомним сначала, что называется скалярным произведением и каким образом его можно находить.
Скалярным произведением двух векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.
Математически это может выглядеть следующим образом:
$\overline{δ}\overline{β}=|\overline{δ}||\overline{β}|cos∠(\overline{δ},\overline{β})$
Также, помимо того, как из самого определения 1, для нахождения скалярного произведения можно пользоваться следующей теоремой.
Скалярное произведение двух данных векторов $\overline{δ}$ и $\overline{β}$ с координатами $(δ_1,β_1,γ_1)$ и $(δ_2,β_2,γ_2)$, равняется сумме произведений их соответствующих координат.
Математически выглядит следующим образом
$\overline{δ}\cdot \overline{β}=δ_1 δ_2+β_1 β_2+γ_1 γ_2$
Обозначение: $\overline{δ}\cdot \overline{β}$.
С помощью скалярного произведения мы можем найти косинус угла между векторами. Пусть нам даны векторы $\overline{δ}$ и $\overline{β}$ с координатами $(δ_1,β_1,γ_1)$ и $(δ_2,β_2,γ_2)$, соответственно. Из определения 2 получим, что
$cos∠(\overline{δ},\overline{β})=\frac{\overline{δ}\cdot \overline{β}}{|\overline{δ}||\overline{β}|}$
Из теоремы 1 мы знаем, что $\overline{δ}\cdot \overline{β}=δ_1 δ_2+β_1 β_2+γ_1 γ_2$, следовательно
$cos∠(\overline{δ},\overline{β})=\frac{δ_1 δ_2+β_1 β_2+γ_1 γ_2}{|\overline{δ}||\overline{β}|}$
Расписывая по формуле длины вектора значения $|\overline{δ}|$ и $|\overline{β}|$, окончательно получим
$cos∠(\overline{δ},\overline{β})=\frac{δ_1 δ_2+β_1 β_2+γ_1 γ_2}{\sqrt{δ_1^2+β_1^2+γ_1^2 } \sqrt{δ_2^2+β_2^2+γ_2^2}}$
Найдя значение косинуса, мы легко найдем и значение самого угла.
Найти косинус угла между векторами $\overline{δ}$ и $\overline{β}$, имеющими координаты $(1,-2,2)$ и $(3,0,4)$, соответственно.
Решение.
Найдем скалярное произведение между данными векторами через координаты:
$\overline{δ}\cdot \overline{β}=1\cdot 3+(-2)\cdot 0+2\cdot 4=11$
Найдем длины этих векторов:
$|\overline{δ}|=\sqrt{1^2+(-2)^2+2^2}=\sqrt{9}=3$
$|\overline{β}|=\sqrt{3^2+0^2+4^2}=\sqrt{25}=5$
В результате, получим
$cos∠(\overline{δ},\overline{β})=\frac{11}{3\cdot 5}=\frac{11}{15}$
Ответ: $\frac{11}{15}$.
Нахождение угла между векторами с помощью векторного произведения
Вспомним сначала, определение векторного произведения и каким образом его можно находить.
Векторным произведением двух векторов называется такой вектор, который будет перпендикулярен обоим данным векторам, и его длина равна произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.
Обозначение: $\overline{δ}х\overline{β}$.
Математически это выглядит следующим образом:
- $|\overline{δ}х\overline{β}|=|\overline{δ}||\overline{β}|sin∠(\overline{δ},\overline{β})$
- $\overline{δ}х\overline{β}⊥\overline{δ}$, $\overline{δ}х\overline{β}⊥\overline{β}$
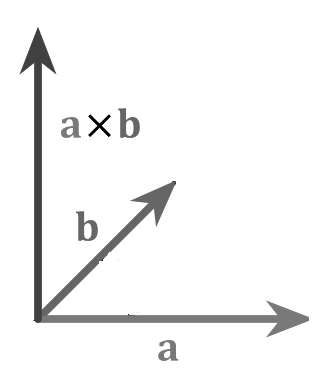
- $(\overline{δ}х\overline{β},\overline{δ},\overline{β})$ и $(\overline{i},\overline{j},\overline{k})$ одинаково ориентированы (рис. 2)
Рисунок 2. Векторное произведение. Автор24 — интернет-биржа студенческих работ
Для нахождения вектора векторного произведения можно пользоваться следующей формулой:
$\overline{δ}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\δ_1&δ_2&δ_3\\β_1&β_2&β_3\end{vmatrix}$
С помощью векторного произведения мы можем найти синус угла между данными векторами. Пусть нам даны векторы $\overline{δ}$ и $\overline{β}$ с координатами $(δ_1,δ_2,δ_3)$ и $(β_1,β_2,β_3)$, соответственно. Из определения 3 получим, что
${\sin \angle \left(\overrightarrow{\delta },\overrightarrow{\beta }\right)\ }=\frac{\left|\overrightarrow{\delta }х\overrightarrow{\beta }\right|}{\left|\overrightarrow{\delta }\right||\overrightarrow{\beta }|}$
Найдем вектор векторного произведения по формуле:
$\overline{δ}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\δ_1&δ_2&δ_3\\β_1&β_2&β_3\end{vmatrix}=(δ_2 β_3-δ_3 β_2,δ_3 β_1-δ_1 β_3,δ_1 β_2-δ_2 β_1)$
Расписывая по формуле длины вектора значения $|\overline{δ}|$, $|\overline{β}|$ и $|\overline{δ}х\overline{β}|$, окончательно получим
$sin∠(\overline{δ},\overline{β})=\frac{\sqrt{(δ_2 β_3-δ_3 β_2)^2+(δ_3 β_1-δ_1 β_3)^2+(δ_1 β_2-δ_2 β_1)^2}}{\sqrt{δ_1^2+δ_2^2+δ_3^2}\sqrt{β_1^2+β_2^2+β_3^2}}$
Найдя значение синуса, мы легко найдем и значение самого угла между векторами через координаты через формулу.
Найти синус угла между векторами $\overline{δ}$ и $\overline{β}$, имеющими координаты $(1,-2,2)$ и $(3,0,4)$, соответственно.
Решение.
Найдем вектор векторного произведения между данными векторами по формуле:
$\overline{δ}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\1&-2&2\\3&0&4\end{vmatrix}=-8\overline{i}+2\overline{j}+6\overline{k}=(-8,1,6)$
Найдем длины этих векторов:
$|\overline{δ}х\overline{β}|=\sqrt{(-8)^2+2^2+6^2}=\sqrt{104}=2\sqrt{26}$
$|\overline{δ}|=\sqrt{1^2+(-2)^2+2^2}=\sqrt{9}=3$
$|\overline{β}|=\sqrt{3^2+0^2+4^2}=\sqrt{25}=5$
В результате, получим
$sin∠(\overline{δ},\overline{β})=\frac{2\sqrt{26}}{3\cdot 5}=\frac{2\sqrt{26}}{15}$
Ответ: $\frac{2\sqrt{26}}{15}$.