Понятие вектора и перпендикулярности векторов
Вначале надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.
Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.
Концами отрезка будем называть точки, которые его ограничивают.
Для введения определения вектора один из концов отрезка назовем его началом.
Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.
Обозначение: $\overline{AB}$ - вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.
Иначе одной маленькой буквой: $\overline{a}$ (рис. 1).
Нулевым вектором будем называть любую точку, которая принадлежит плоскости.
Обозначение: $\overline{0}$.
Введем теперь, непосредственно, определение коллинеарных векторов.
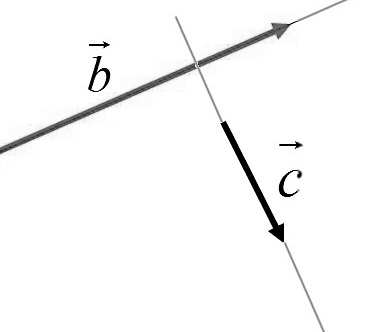
Два ненулевых вектора будем называть перпендикулярными (ортогональными), если они лежат на каких-либо перпендикулярных прямых (рис.2).
Также введем определение скалярного произведения, которое будет нам необходимо далее.
Скалярным произведением двух данных векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.
Математически это может выглядеть следующим образом:
$\overline{α}\overline{β}=|\overline{α}||\overline{β}|cos∠(\overline{α},\overline{β})$
Скалярное произведение также можно найти с помощью координат векторов следующим образом
$\overline{α}\overline{β}=α_1 β_1+α_2 β_2+α_3 β_3$
Признак перпендикулярности через пропорциональность
Чтобы ненулевые векторы были перпендикулярны между собой, необходимо и достаточно, чтобы их скалярное произведение этих векторов равнялось нулю.
Доказательство.
Необходимость: Пусть нам даны векторы $\overline{α}$ и $\overline{β}$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они перпендикулярны друг другу. Тогда нам нужно доказать следующее равенство
$\overline{α}\cdot \overline{β}=0$
Так как векторы $\overline{α}$ и $\overline{β}$ перпендикулярны, то угол между ними равняется $90^0$. Найдем скалярное произведение данных векторов по формуле из определения 6.
$\overline{α}\cdot \overline{β}=|\overline{α}||\overline{β}|cos90^\circ =|\overline{α}||\overline{β}|\cdot 0=0$
Достаточность: Пусть верно равенство $\overline{α}\cdot \overline{β}=0$. Докажем, что векторы $\overline{α}$ и $\overline{β}$ будут перпендикулярны друг другу.
По определению 6, будет верно равенство
$|\overline{α}||\overline{β}|cos∠(\overline{α},\overline{β})=0$
$cos∠(\overline{α},\overline{β})=0$
$∠(\overline{α},\overline{β})=90^\circ$
Следовательно, векторы $\overline{α}$ и $\overline{β}$ будут перпендикулярны друг другу.
Теорема доказана.
Доказать, что векторы с координатами $(1,-5,2)$ и $(2,1,3/2)$ перпендикулярны.
Доказательство.
Найдем скалярное произведение для этих векторов через формулу, данную выше
$\overline{α}\cdot \overline{β}=1\cdot 2+(-5)\cdot 1+2\cdot \frac{3}{2}=2\cdot 5+3=0$
Значит, по теореме 1, эти вектор перпендикулярны.
Нахождение перпендикулярного вектора к двум данным векторам через векторное произведение
Введем вначале понятие векторного произведения.
Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.
Обозначение: $\overline{α}х\overline{β}$.
Чтобы найти векторное произведение, будем пользоваться формулой
$\overline{α}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\α_1&α_2&α_3\\β_1&β_2&β_3\end{vmatrix}$
Так как вектор векторного произведения двух векторов перпендикулярен обоим этим векторам, то он и будет иском вектором. То есть, для того, чтоб найти перпендикулярный для двух векторов вектор, нужно просто найти их векторное произведение.
Найти вектор, перпендикулярный к векторам с координатами $\overline{α}=(1,2,3)$ и $\overline{β}=(-1,0,3)$
Решение.
Найдем векторное произведение данных векторов.
$\overline{α}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\1&2&3\\-1&0&3\end{vmatrix}=(6-0)\overline{i}-(3+3)\overline{j}+(0+2)\overline{k}=6\overline{i}-6\overline{j}+2\overline{k}=(6,6,2)$