Решение неравенств с двумя неизвестными, а тем более их системы, на первый взгляд кажется сложной задачей. Рассмотрим алгоритм, с помощью которого можно легко справиться с этой задачей.
Неравенство с двумя неизвестными
Пусть имеется неравенство с двумя неизвестными вида $y $, $\le$, $\ge$).
Множество решений подобного неравенства можно изобразить на координатной плоскости. Для этого необходимо:
- Построить график функции y=f(x), который разобьет координатную плоскость на две разные области.
-
Выбрать одну из этих областей и рассмотреть в ней любую точку. Проверить, выполняется ли для этой точки исходное неравенство:
- Если неравенство выполняется, следовательно, оно выполняется и для всей области, из которой выбирали точку. Таким образом, область, в которой лежит выбранная точка и есть множеством решений неравенства.
- Если неравенство не выполняется, то множество решений неравенства – область, в которой не лежит выбранная точка.
-
При решении строгих неравенств границы области, которыми являются точки графика функции $y=f(x)$, не включаются в множество решений, при этом граница изображается пунктирной линией. При нестрогих неравенствах границы области включаются в множество решений неравенства, при этом граница изображается сплошной линией.
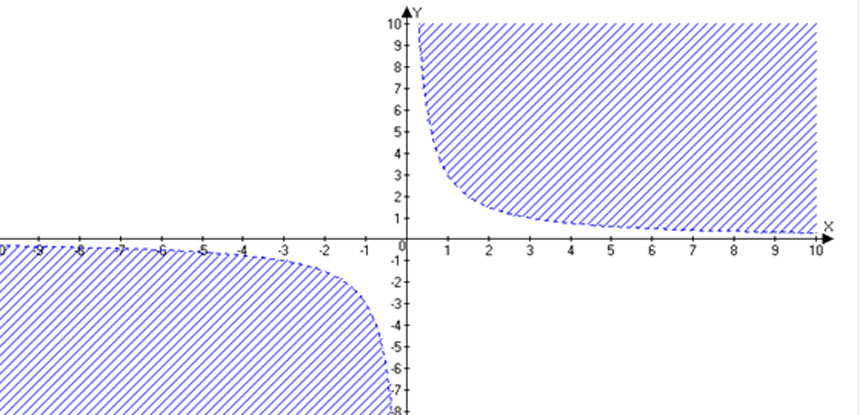
Показать на графике множество точек, которое задается неравенством $xy>3$.
Решение.
-
Построим график функции $xy=3$. Для этого разделим обе части уравнения на $х$, т.к. оно не может обращаться в нуль, что следует из уравнения (произведение числа на нуль не может равняться $3$):
$y=\frac{3}{x}$.
График получившейся функции – гипербола, которая разобьет координатную плоскость на 2 области: одна находится между ветвями гиперболы, а другая – за ними.
-
Выберем из одной области любую точку, например, с координатами $(1; 2)$.
Подставим ее координаты в неравенство:
$xy>3$;
$1 \cdot 2 > 3$;
$2>3$ – неравенство неверное.
Следовательно, точки выбранной области не являются решением данного неравенства. Таким образом, решением неравенства будет другая область, из которой точку не выбирали.
-
Данное неравенство строгое, поэтому граничные точки, которыми являются точки графика функции y=3/x, наносятся на график пунктирной линией. Обозначим на графике множество точек, которые являются решением данного неравенства:
Система неравенств с двумя неизвестными
Рассмотрим пример решения системы неравенств с двумя неизвестными.
Показать на графике множество точек, которое задается системой неравенств
\[\left\{ \begin{array}{c} {x^2+y^2\le 49,} \\ {2x+y >5.} \end{array} \right..\]Решение.
Построим графики функций, которые соответствуют данным неравенствам:
$x^2+y^2=49$ – окружность с радиусом $7$;
$2х+y=5$ – прямая.
Изображаем функцию $x^2+y^2=49$ сплошной линией, т.к. она соответствует нестрогому неравенсту, а прямую $2х+y=5$ – пунктирной.
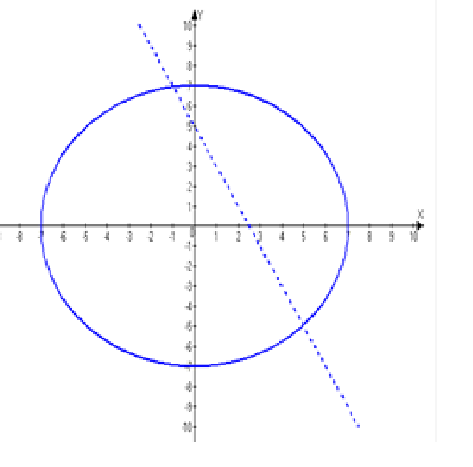
Рассмотрим каждое неравенство отдельно.
Первое неравенство $x^2+y^2 \le 49$:
Возьмем точку $(5; 8)$ выше графика данной функции. Проверим справедливость неравенства:
$5^2+8^2 \le 49$,
$89≤49$ – неравенство неверно.
Следовательно, решение данного неравенства – область, в которой не лежит выбранная точка, т.е. область внутри окружности.
Второе неравенство $2x+y > 5$:
Возьмем точку $(4; 3)$ выше графика данной функции. Проверим справедливость неравенства:
$2 \cdot 4+3 > 5$,
$11 > 5$ – неравенство верно.
Следовательно, решение данного неравенства – область, в которой лежит выбранная точка, т.е. область выше прямой.
Изобразим найденные решения на координатной плоскости.
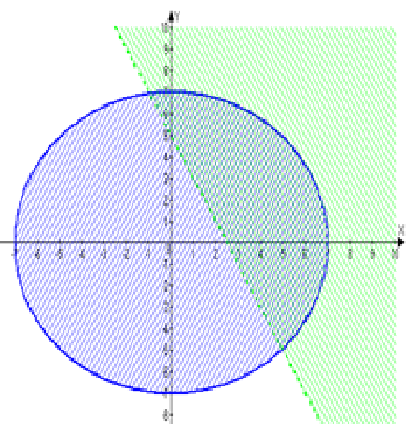
Пересечение полученных областей и является решением данной системы.