Одним из частных случаев систем неравенств с двумя переменными являются системы линейных неравенств с двумя переменными. Рассмотрим их.
Системы линейных неравенств с двумя переменными
Введем сначала все необходимые понятия.
Неравенства вида ax+by≤()c, где x и y -- неизвестные переменные, а a, b и c -- некоторые числа, причем a и b отличны от нуля называются линейными неравенствами с двумя переменными.
Пара чисел называется решением линейного неравенства с двумя переменными, если при их подстановке в уравнение получается верное равенство.
Графиком линейного неравенства с двумя переменными является множество всех точек, которые является решением данного линейного неравенства.
Системой линейных неравенств с двумя переменными называется такая система неравенств, которая в своем составе имеет два и более линейных неравенств с двумя переменными.
Решением системы линейных неравенств называется такая пара чисел, которая является решением всех неравенств, входящих в данную систему.
Рассмотрим решение систем линейных неравенств с двумя переменными на примере.
Решить систему неравенств
\[\left\{ \begin{array}{c} {yРешение.Решим для начала оба неравенства отдельно.
-
$y
Изобразим график линейного неравенства (рис. 1).
-
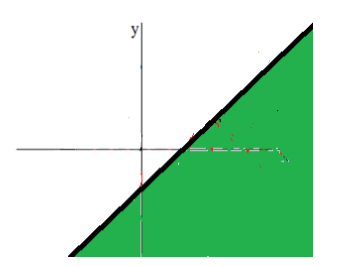
$y
Изобразим график линейного неравенства (рис. 2).
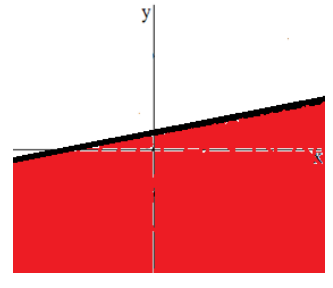
Рисунок 2. Решение неравенства $y -
Изобразим теперь общее решение системы линейных неравенств:
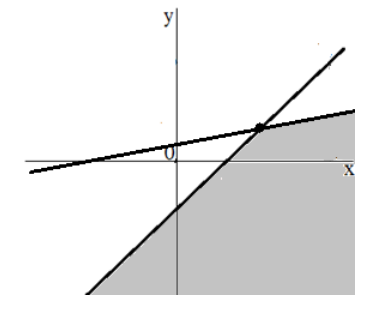
Рисунок 3.
Примеры других неравенств с двумя переменными
Рассмотрим другие примеры систем неравенств с двумя переменными.
Решить систему неравенств
{x2+y2≥4, x2+y2≤9Решение.
Решим для начала два этих неравенства по отдельности
-
x2+y2≥4
x2+y2=4 -- окружность с центром в точке (0,0) и радиусом 2. Изобразим график неравенства
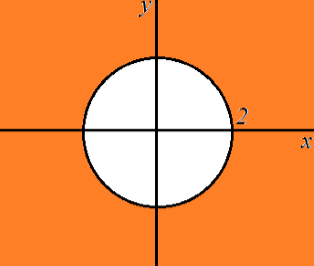
Рисунок 4. -
x2+y2≤9
x2+y2=9 -- окружность с центром в точке (0,0) и радиусом 3. Изобразим график неравенства
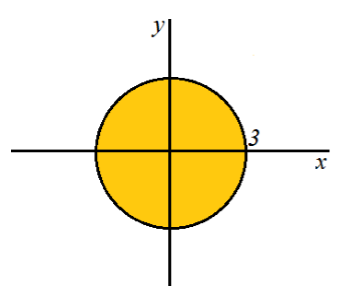
Рисунок 5. -
Изобразим теперь общее решение:
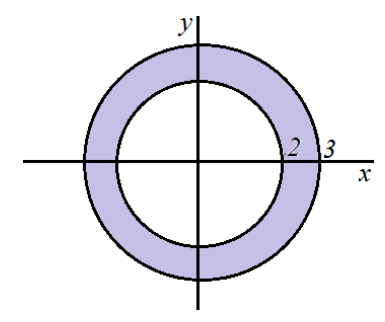
Рисунок 6.
