Примеры решения производных

На рисунке 1 изображен график функции и касательной к графику в точке с абсциссой x0. Найти значение производной функции в абсциссе.

Решение. Производная в точке равна отношению~приращения функции к приращению аргумента. Выберем на касательной две точки с целочисленными координатами. Пусть, например, это будут точки F (-2,0) и C (-3,2).

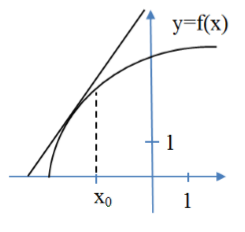
Рисунок 1. График функции

Найдем приращение аргумента:

$\Delta $x = х2 -- х1 = -3 -- (-2) = -1

Найдем приращение функции:

$\Delta $y = y2 -- y1 = 2 -- 0 = 2

Тогда значение производной:

\[\frac{\Delta y}{\Delta x} =-\frac{2}{1} =-2\]

На рисунке 2 изображен график функции. Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 6. Найдите значение производной функции в точке $x_0=6$.

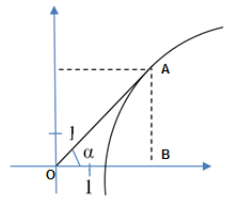
Рисунок 2. График функции

Решение.

Обозначим границы треугольника точками О, А, В и найдем тангенс угла $\alpha $.

\[tg\alpha =tgAOB=\frac{AB}{OB} =\frac{9}{6} =1,5\]

Найти производную функции

\[f(x)=x^{2} -x+2\]

Решение.

1. Добавим к функции приращение
\[\frac{\Delta y}{\Delta x} =\frac{(x+\Delta x)^{2} -(x+\Delta x)+2-x^{2} +x-2}{\Delta x} =\]
2. Выполним алгебраические преобразования в числителе
\[=\frac{x^{2} +2x\Delta x+\Delta x^{2} -x-\Delta x+2-x^{2} +x-2}{\Delta x} =\frac{2x\Delta x+\Delta x^{2} -\Delta x}{\Delta x} =\]

Произведем сокращение дроби \[=\frac{\Delta x\left(2x+\Delta x-1\right)}{\Delta x} =2x+\Delta x-1\]

3. Найдем предел приращения при его стремлении к 0:
\[f`(x)=\mathop{\lim }\limits_{\Delta x\to 0} \frac{\Delta y}{\Delta x} =2x+0-1=2x-1\]

Вычислить по таблице производную функции

\[y=x^{3} +3x^{2} -1\]

Решение.

Производная суммы/разности равна производной всех элементов выражения

\[y`=3x^{2} +3\cdot 2\cdot x^{1} =3x^{2} +6x\]

Вычислить по таблице производную функции

\[y=\frac{2x^{4} -x^{2} -1}{x-1} \]

Решение.

По формуле разности функций вычислим производную

\[y'=\left(\frac{f\left(x\right)}{g\left(x\right)} \right)^{{'} } =\frac{f\left(x\right)^{{'} } g\left(x\right)-g\left(x\right)^{{'} } f\left(x\right)}{g^{2} \left(x\right)} \]

За f(x) примем числитель, а за g(x) - знаменатель

\[y`=\frac{\left(2x^{4} -x^{2} -1\right)`\left(x-1\right)-\left(2x^{4} -x^{2} -1\right)\left(x-1\right)`}{\left(x-1\right)^{2} } =\]

Найдем производные отдельные множителей и упростим дробь

\[=\frac{\left(2\cdot 4\cdot x^{3} -2x\right)\cdot \left(x-1\right)-\left(2x^{4} -x^{2} -1\right)}{x^{2} -2x+1} =\frac{8x^{4} -2x^{2} -8x^{3} +2x-2x^{4} +x^{2} +1}{x^{2} -2x+1} =\] \[=\frac{6x^{4} -8x^{3} -x^{2} +2x+1}{x^{2} -2x+1} =\frac{(6x^{2} +4x+1)(x^{2} -2x+1)}{x^{2} -2x+1} =6x^{2} +4x+1\]

Найти производную тригонометрической функции y = tgx

Решение.

\[y`=\left(\frac{\sin x}{\cos x} \right)`=\frac{\left(\sin x\right)`\cos x-\left(\cos x\right)`\sin x}{\cos ^{2} x} =\frac{\cos ^{2} x+\sin ^{2} x}{\cos ^{2} x} =\frac{1}{\cos ^{2} x} \]