Производная характеризует скорость изменения функции в определенной точке. На рисунке 1 изображена производная функции на координатной плоскости.
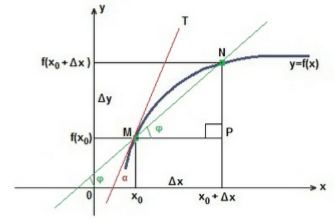
Рисунок 1. Производная функции
Формулы нахождения производной
1) Производная постоянного значения равна 0
Найти производную
\[y=3\]Решение:
\[y'=3'=0\]2) Производная неизвестной величины равна единице
\[x'=1\]3) Если выражение содержит постоянную величину -- ее необходимо вынести за знак предела.
\[y'=\left(c\cdot f\left(x\right)\right)^{{'} } =c\cdot f'\left(x\right)\]Найти производную
\[y=3x\]Решение:
\[y'=\left(3x\right)^{{'} } =3x'=3\cdot 1=3\]4) Производная степенной функции находится как произведение значения степени на степенное выражение, степень которого уменьшена на 1.
\[y'=\left(x^{n} \right)^{{'} } =n\cdot x^{n-1} \]Найти производную
\[y=2x^{5} \]Решение:
\[y'=\left(2x^{5} \right)^{{'} } =2(x^{5} )'=2\cdot 5\cdot x^{5-1} =10\cdot x^{4} \]5) Производная экспоненты равна самой экспоненте
6) Производная числа в степени х равна произведения данного выражения на логарифм числа:
\[y'=\left(a^{x} \right)^{{'} } =a^{x} \cdot \log a\]Найти производную
\[y=10^{x} \]Решение:
\[y'=\left(10^{x} \right)^{{'} } =10^{x} \cdot \log 10=10^{x} \cdot 1=10^{x} \]7) Производная sinx равна cosx
8) Производная cosx равна --sinx
9) Производная тангенса равна частному единицы и квадратному косинусу х
\[y'=\left(tgx\right)^{{'} } =\frac{1}{\cos ^{2} x} \]10) Производная котангенса равна частному минус единицы и квадратному синусу х
\[y'=\left(ctgx\right)^{{'} } =-\frac{1}{\sin ^{2} x} \]11) Производная арксинуса равна:
\[y'=\left(\arcsin x\right)^{{'} } =\frac{1}{\sqrt{1-x^{2} } } \]12) Производная арккосинуса равна:
\[y'=\left(\arccos x\right)^{{'} } =-\frac{1}{1-x^{2} } \]13) Производная арктангенса равна:
\[y'=\left(arctgx\right)^{{'} } =\frac{1}{1+x^{2} } \]14) Производная арккотангенса противоположна производной арктангенса и равна:
\[y'=\left(arctgx\right)^{{'} } =-\frac{1}{1+x^{2} } \]15) Производная суммы функций равна сумме их производных:
\[\left(x+y+...+z\right)^{{'} } =x'+y'+...+z'\]Найти производную
\[y=10^{x} \]Решение:
\[y'=\left(10^{x} \right)^{{'} } =10^{x} \cdot \log 10=10^{x} \cdot 1=10^{x} \]16) Производная произведения нескольких функций равна:
$y' = (fx1 \cdot fx2 \cdot \dots \cdot fxn) = fx'1fx2fx3\dots fxn + fx1fx'2fx3\dots fxn + \dots + fx1fx2fx3\dots fx'n$
17) Производная частного вычисляется по формуле:
\[y'=\left(\frac{f\left(x\right)}{g\left(x\right)} \right)^{{'} } =\frac{f\left(x\right)^{{'} } g\left(x\right)-g\left(x\right)^{{'} } f\left(x\right)}{g^{2} \left(x\right)} \]Найти производную
\[y=\sin x\cdot \cos x\cdot tgx\cdot ctgx\]Решение:
\[y'=\left(\sin x\cdot \cos x\cdot tgx\right)^{{'} } =\sin x'\cdot \cos x\cdot tgx+\sin x\cdot \cos x'\cdot tgx+\sin x\cdot \cos x\cdot tgx'=y'=\cos x\cdot \cos x\cdot tgx-\sin x\cdot \sin x\cdot tgx+\sin x\cdot \frac{\cos x}{\cos ^{2} x} =\cos ^{2} x\cdot tgx-\sin x^{2} \cdot tgx+\frac{\sin x}{\cos x} =\] \[y'=tgx\left(\cos ^{2} x-\sin x^{2} \right)+tgx=tgx+tgx=2tgx\]Найти производную
\[y=\frac{2x^{2} -3}{x^{3} } \]Решение:
\[y'=\left(\frac{2x^{2} -3}{x^{3} } \right)^{{'} } =\frac{x^{3} \cdot \left(2x^{2} -3\right)^{{'} } -\left(x^{3} \right)^{{'} } \cdot \left(2x^{2} -3\right)}{\left(x^{3} \right)^{2} } =\frac{x^{3} \cdot 4x-3x^{2} \cdot \left(2x^{2} -3\right)}{\left(x^{3*2} \right)^{} } =\frac{4x^{4} -6x^{4} -9x^{2} }{x^{3*2} } =\] \[y'=\frac{-2x^{4} -9x^{2} }{x^{5} } =\frac{-x^{2} (2x^{2} +9)}{x^{3*2} } =-\frac{2x^{2} +9}{x^{3} } \]











