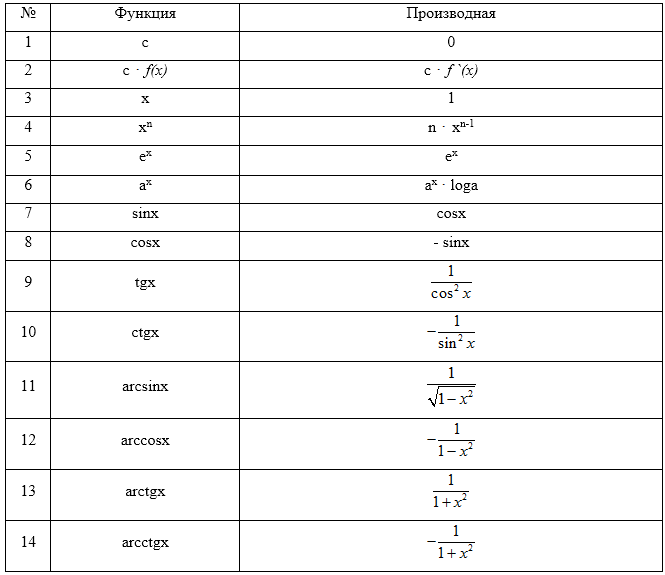
Дифференцирование -- это определение производной.
По формулам дифференцирования найти производную функции
Решение.
- Вынесем числовой множитель за знак производной \[y'=\left(\frac{3x^{8} }{24} \right){{'} } =\frac{3}{24} \left(x^{8} \right){{'} } \]
- Найдем производную функции в степени по формуле: \[\left(x^{n} \right){{'} } =n\cdot x^{n-1} \] \[y'=\frac{3}{24} \left(x^{8} \right){{'} } =\frac{3}{24} \cdot 8\cdot x^{8-1} =\frac{24}{24} \cdot x^{7} =x^{7} \]
По формулам дифференцирования найти производную функции в точке х=0.
\[y=\frac{4arcctgx}{6} \]Решение.
- Вынесем числовой множитель за знак производной \[y'=\left(\frac{4arcctgx}{6} \right){{'} } =\frac{4}{6} arcctgx'\]
- Найдем производную тригонометрической функции по формуле: \[\left(arcctgx\right){{'} } =\frac{1}{1+x^{2} } \] \[y'=\frac{4}{6} arcctgx'=\frac{4}{6} \cdot \frac{1}{1+x^{2} } \]
- Заменим х числом 0 (по условию) \[y(0)'=\frac{4}{6} \cdot \frac{1}{1+x^{2} } =\frac{4}{6} \cdot \frac{1}{1+0} =\frac{4}{6} =\frac{2}{3} \]
По формулам дифференцирования найти производную функции в точке х=1/12
\[y=-2e^{12x} \]Решение.
- Вынесем числовой множитель за знак производной \[y'=\left(-2e^{12x} \right){{'} } =-2\left(e^{12x} \right){{'} } \]
- Найдем производную функции по формуле: \[e^{x} {{'} } =e^{x} \] \[y'=-2\left(e^{12x} \right){{'} } =-2e^{12x} \]
- Заменим х числом 1/12 (по условию) \[y'=-2e^{12x} =-2e^{12\cdot \frac{1}{12} } =-2e\]
По формулам дифференцирования найти производную функции в точке х=$\pi $
\[y=8\sin x-\cos x\]Решение.
- Найдем производную каждого члена функции \[y'=\left(8\sin x-\cos x\right){{'} } =8\left(\sin x\right){{'} } -\left(\cos x\right){{'} } =\]
- Найдем производные по формулам: \[\sin x'=\cos x\] \[\cos x'=-\sin x\] \[y'=8\left(\sin x\right){{'} } -\left(\cos x\right){{'} } =8\cos x-(-\sin x)=8\cos x+\sin x\]
- Заменим х значением $\pi $ (по условию) \[y'=8\cos \pi +\sin \pi =8\cdot \left(-1\right)+0=-8\]
По формулам дифференцирования найти производную функции
\[y=\frac{1}{\sqrt[{3}]{x^{2} } } \]Решение.
- Представим корень в виде степени функции $х$ \[y`=\left(x^{-\frac{2}{3} } \right){{'} } \]
- Вычислим производную степени функции по формуле: \[\left(x^{n} \right){{'} } =n\cdot x^{n-1} \] \[y'=-\frac{2}{3} x^{-\frac{2}{3} -1} =-\frac{2}{3} x^{-\frac{2}{3} -\frac{3}{3} } =-\frac{2}{3} x^{-\frac{5}{3} } =-\frac{2}{3x\sqrt[{3}]{x^{2} } } \]